题目内容
7.约分:(1)$\frac{2a{xy}^{2}}{6{ax}^{2}y}$=$\frac{y}{3x}$;(2)$\frac{{x}^{4}{-y}^{4}}{{x}^{4}-{2x}^{2}y^{2}{+y}^{4}}$=$\frac{{x}^{2}+{y}^{2}}{{x}^{2}-{y}^{2}}$.分析 (1))约去分子与分母的公因式;
(2))约去分子与分母的公因式.
解答 解::(1)$\frac{2a{xy}^{2}}{6{ax}^{2}y}$=$\frac{y}{3x}$;
(2)$\frac{{x}^{4}{-y}^{4}}{{x}^{4}-{2x}^{2}y^{2}{+y}^{4}}$=$\frac{{x}^{2}+{y}^{2}}{{x}^{2}-{y}^{2}}$,
故答案为:$\frac{y}{3x}$;$\frac{{x}^{2}+{y}^{2}}{{x}^{2}-{y}^{2}}$.
点评 本题考查了分式的约分,解题的关键是确定分子与分母的公因式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列图形中,是中心对称图形但不是轴对称图形的是( )
| A. |  | B. | 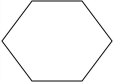 | C. | 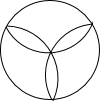 | D. | 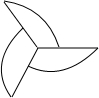 |
2.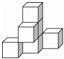 下列图形不是图中几何体的三视图的是( )
下列图形不是图中几何体的三视图的是( )
 下列图形不是图中几何体的三视图的是( )
下列图形不是图中几何体的三视图的是( )| A. | 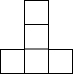 | B. | 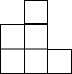 | C. | 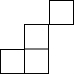 | D. | 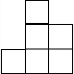 |
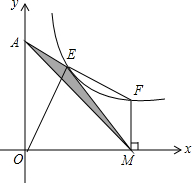 如图,E,F在双曲线y=$\frac{8}{x}$上,FE交y轴于点A,AE=EF,FM⊥x轴于M,求S△AME.
如图,E,F在双曲线y=$\frac{8}{x}$上,FE交y轴于点A,AE=EF,FM⊥x轴于M,求S△AME.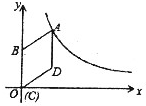 如图,在平面直角坐标系中,菱形ABCD的顶点C与远点O重合,点B在y轴的正半轴上,点A在反比例函数$y=\frac{k}{x}(k>0,x>0)$的图象上,点D的坐标为(4,3),则k的值为( )
如图,在平面直角坐标系中,菱形ABCD的顶点C与远点O重合,点B在y轴的正半轴上,点A在反比例函数$y=\frac{k}{x}(k>0,x>0)$的图象上,点D的坐标为(4,3),则k的值为( )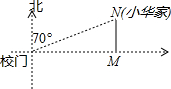 如图,小华家位于校门北偏东70°的方向,和校门的直线距离为4km的N处,则小华家到校门所在街道(东西方向)的距离NM约为1.37km.(用科学计算器计算,结果精确到0.01km).
如图,小华家位于校门北偏东70°的方向,和校门的直线距离为4km的N处,则小华家到校门所在街道(东西方向)的距离NM约为1.37km.(用科学计算器计算,结果精确到0.01km).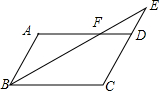 如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,若ED:DC=2:3,△DEF的面积为8,则平行四边形ABCD的面积为60.
如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,若ED:DC=2:3,△DEF的面积为8,则平行四边形ABCD的面积为60.