题目内容
10.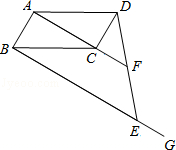 如图,在平行四边形ABCD中,过点B作BE∥AC,在BG上取点E,连接DE交AC的延长线于点F.
如图,在平行四边形ABCD中,过点B作BE∥AC,在BG上取点E,连接DE交AC的延长线于点F.(1)求证:DF=EF;
(2)如果AD=6,∠ADC=60°,AC⊥DC于点C,AC=2CF,求BE的长.
分析 (1)连接BD交AC于点O.由平行四边形的性质可知O为BD中点,又因为BG∥AF,进而证明DF=EF.
(2)利用直角三角形的性质和三角形中位线性质定理以及平行四边形的性质即可求出BE的长.
解答 (1)证明:连接BD交AC于点O.
∵四边形ABCD是平行四边形,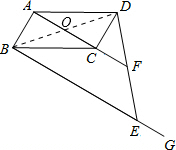
∴OB=OD,
∵BG∥AF,
∴DF=EF;
(2)解:∵AC⊥DC,∠ADC=60°,AD=6,
∴AC=4$\sqrt{3}$.
∵OF是△DBE的中位线,
∴BE=2OF.
∵OF=OC+CF,
∴BE=2OC+2CF.
∵四边形ABCD是平行四边形,
∴AC=2OC.
∵AC=2CF,
∴BE=2AC=8$\sqrt{3}$.
点评 本题考查了平行四边形的性质、三角形的中位线定理以及在直角三角形中30°所对的直角边是斜边的一半和勾股定理的运用.

练习册系列答案
相关题目
15.下列图形中,是中心对称图形但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. | 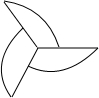 |
2.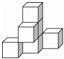 下列图形不是图中几何体的三视图的是( )
下列图形不是图中几何体的三视图的是( )
 下列图形不是图中几何体的三视图的是( )
下列图形不是图中几何体的三视图的是( )| A. | 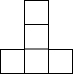 | B. | 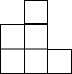 | C. | 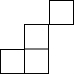 | D. | 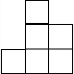 |
19.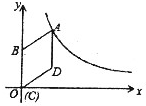 如图,在平面直角坐标系中,菱形ABCD的顶点C与远点O重合,点B在y轴的正半轴上,点A在反比例函数$y=\frac{k}{x}(k>0,x>0)$的图象上,点D的坐标为(4,3),则k的值为( )
如图,在平面直角坐标系中,菱形ABCD的顶点C与远点O重合,点B在y轴的正半轴上,点A在反比例函数$y=\frac{k}{x}(k>0,x>0)$的图象上,点D的坐标为(4,3),则k的值为( )
 如图,在平面直角坐标系中,菱形ABCD的顶点C与远点O重合,点B在y轴的正半轴上,点A在反比例函数$y=\frac{k}{x}(k>0,x>0)$的图象上,点D的坐标为(4,3),则k的值为( )
如图,在平面直角坐标系中,菱形ABCD的顶点C与远点O重合,点B在y轴的正半轴上,点A在反比例函数$y=\frac{k}{x}(k>0,x>0)$的图象上,点D的坐标为(4,3),则k的值为( )| A. | 20 | B. | 32 | C. | 24 | D. | 27 |
20.若a=$\sqrt{3b-1}$-$\sqrt{1-3b}$+6,则ab的算术平方根是( )
| A. | 2 | B. | $\sqrt{2}$ | C. | ±$\sqrt{2}$ | D. | 4 |
 如图,已知在△ABC中,∠ACB=90°,D为BC上一点,DE⊥AB,若∠DCE=∠DEC,已知CD=$\frac{3}{2}$,BC=4
如图,已知在△ABC中,∠ACB=90°,D为BC上一点,DE⊥AB,若∠DCE=∠DEC,已知CD=$\frac{3}{2}$,BC=4 如图,?ABCD中,过D的直线交AC,AB及CB的延长线于E,F,G.
如图,?ABCD中,过D的直线交AC,AB及CB的延长线于E,F,G.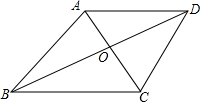 菱形ABCD的边长为6,∠ABC=60°,点P是菱形内一点,且PA=PC=2$\sqrt{3}$
菱形ABCD的边长为6,∠ABC=60°,点P是菱形内一点,且PA=PC=2$\sqrt{3}$