Question

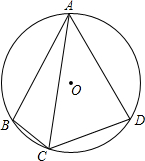已知：A、B、C、D共圆，AB=AD，∠BAD=60°，AC=a，求S_{四边形ABCD}．

Answer 1

考点：旋转的性质,全等三角形的判定与性质,圆周角定理

专题：

分析：如图，作辅助线；首先证明△ABM≌△ADN；同理可证：△ACM≌△ACN，得到S_{四边形ABCD}=2S_△ACN；求出CN、AN的长度，即可解决问题．

解答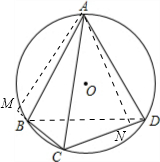：解：如图，过点A作AN⊥CD，AM⊥CB，交CB的延长线于点M；
∵AB=AD，∠BAD=60°，
∴△ABD为等边三角形，
∴∠ABD=∠ADB=60°，
∴∠ACD=∠ABD=60°，∠ACB=∠ADB=60°，
∴AC平分∠BCD，AM=AN；
在△ABM与△ADN中，

AB=AD AM=AN

，
△ABM≌△ADN（HL），
同理可证：△ACM≌△ACN，
∴S_{四边形ABCD}=2S_△ACN；
在△ACN中，sin60°=

AN

AC

，cos60°=

CN

AC

，
∴AN=

3

2

a，CN=

1

2

a，
∴S_{四边形ABCD}=2×

1

2

•CN•AN=

3

4

a2．

点评：该题主要考查了全等三角形的判定及其性质、等边三角形的判定及其性质、角平分线的性质等几何知识点及其应用问题；解题的关键是作辅助线，构造全等三角形．