题目内容
9.解方程组:$\left\{\begin{array}{l}{x+y-z=0}\\{x+2y-z=3}\\{2x-3y+2z=5}\end{array}\right.$.分析 先用②-①得出y的值,再用②×2+③得出4x+y=6 ④,然后把y的值代入④求出x的值,最后把x,y的值代入①,求出z的值,从而求出方程组的解.
解答 解:$\left\{\begin{array}{l}{x+y-z=0①}\\{x+2y-z=3②}\\{2x-3y+2z=③}\end{array}\right.$,
②-①得:y=3,
②×2+③得:4x+y=6 ④,
把y=3代入④得:x=$\frac{3}{4}$,
把x=$\frac{3}{4}$,y=3代入①得:z=$\frac{15}{4}$,
则原方程组的解为:$\left\{\begin{array}{l}{x=\frac{3}{4}}\\{y=3}\\{z=\frac{15}{4}}\end{array}\right.$.
点评 此题考查了三元一次方程组的解法,把“三元”转化为“二元”、把“二元”转化为“一元”的消元的思想方法,从而进一步理解把“未知”转化为“已知”和把复杂问题转化为简单问题的思想方法.解三元一次方程组的关键是消元.解题之前先观察方程组中的方程的系数特点,认准易消的未知数,消去未知数,组成元该未知数的二元一次方程组.

练习册系列答案
相关题目
20.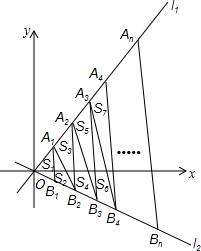 如图,直线l1的解析式为y1=$\sqrt{3}$x,直线l2的解析式为y2=-$\frac{\sqrt{3}}{3}$x,过点(1,0)、(2,0)、(3,0)、(4,0)…(n,0)作y轴的平行线,与直线l1分别交于点A1、A2、A3、A4、…An,与直线l2分别交于点B1、B2、B3、…Bn,连接A1B2、A2B3、A3B4、…、AnBn+1,设△OA1B1的面积为S1,△A1B1B2的面积为S2,△A1B2A2的面积为S3…,则S2015=( )
如图,直线l1的解析式为y1=$\sqrt{3}$x,直线l2的解析式为y2=-$\frac{\sqrt{3}}{3}$x,过点(1,0)、(2,0)、(3,0)、(4,0)…(n,0)作y轴的平行线,与直线l1分别交于点A1、A2、A3、A4、…An,与直线l2分别交于点B1、B2、B3、…Bn,连接A1B2、A2B3、A3B4、…、AnBn+1,设△OA1B1的面积为S1,△A1B1B2的面积为S2,△A1B2A2的面积为S3…,则S2015=( )
 如图,直线l1的解析式为y1=$\sqrt{3}$x,直线l2的解析式为y2=-$\frac{\sqrt{3}}{3}$x,过点(1,0)、(2,0)、(3,0)、(4,0)…(n,0)作y轴的平行线,与直线l1分别交于点A1、A2、A3、A4、…An,与直线l2分别交于点B1、B2、B3、…Bn,连接A1B2、A2B3、A3B4、…、AnBn+1,设△OA1B1的面积为S1,△A1B1B2的面积为S2,△A1B2A2的面积为S3…,则S2015=( )
如图,直线l1的解析式为y1=$\sqrt{3}$x,直线l2的解析式为y2=-$\frac{\sqrt{3}}{3}$x,过点(1,0)、(2,0)、(3,0)、(4,0)…(n,0)作y轴的平行线,与直线l1分别交于点A1、A2、A3、A4、…An,与直线l2分别交于点B1、B2、B3、…Bn,连接A1B2、A2B3、A3B4、…、AnBn+1,设△OA1B1的面积为S1,△A1B1B2的面积为S2,△A1B2A2的面积为S3…,则S2015=( )| A. | $\frac{2016\sqrt{3}}{3}$ | B. | 1008$\sqrt{3}$ | C. | $\frac{2015\sqrt{3}}{2}$ | D. | $\frac{2015\sqrt{3}}{3}$ |
 设函数y1=(x-k)2+k和y2=(x+k)2-k的图象相交于点A,函数y1,y2的图象的顶点分别为B和C.
设函数y1=(x-k)2+k和y2=(x+k)2-k的图象相交于点A,函数y1,y2的图象的顶点分别为B和C.