题目内容
10.计算:(1)(-1)2015-2-2+30
(2)x(x-y)-(x+2y)(2x-y)
分析 (1)首先利用负整数指数幂的性质以及零指数幂的性质和数的乘方运算法则化简求出即可;
(2)直接利用单项式乘以多项式以及多项式乘以多项式运算法则化简求出即可.
解答 解:(1)(-1)2015-2-2+30
=-1-$\frac{1}{4}$+1
=-$\frac{1}{4}$;
(2)x(x-y)-(x+2y)(2x-y)
=x2-xy-(2x2+3xy-2y2)
=-x2-4xy+2y2.
点评 此题主要考查了整式的混合运算以及实数运算,正确掌握相关运算法则是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.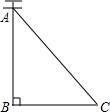 如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )
如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )
 如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )
如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )| A. | $\frac{6}{sin50°}$米 | B. | $\frac{6}{tan50°}$米 | C. | 6cos50°米 | D. | $\frac{6}{cos50°}$米 |
1.若平行四边形中两个内角的度数比为1:2,则其中较小的内角是( )
| A. | 60° | B. | 90° | C. | 120° | D. | 45° |
15.如果分式$\frac{2x}{x-y}$中的x、y都缩小到原来的$\frac{1}{3}$倍,那么分式的值( )
| A. | 扩大到原来的3倍 | B. | 扩大到原来的6倍 | ||
| C. | 不变 | D. | 缩小到原来的$\frac{1}{3}$倍 |
20.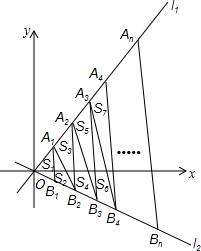 如图,直线l1的解析式为y1=$\sqrt{3}$x,直线l2的解析式为y2=-$\frac{\sqrt{3}}{3}$x,过点(1,0)、(2,0)、(3,0)、(4,0)…(n,0)作y轴的平行线,与直线l1分别交于点A1、A2、A3、A4、…An,与直线l2分别交于点B1、B2、B3、…Bn,连接A1B2、A2B3、A3B4、…、AnBn+1,设△OA1B1的面积为S1,△A1B1B2的面积为S2,△A1B2A2的面积为S3…,则S2015=( )
如图,直线l1的解析式为y1=$\sqrt{3}$x,直线l2的解析式为y2=-$\frac{\sqrt{3}}{3}$x,过点(1,0)、(2,0)、(3,0)、(4,0)…(n,0)作y轴的平行线,与直线l1分别交于点A1、A2、A3、A4、…An,与直线l2分别交于点B1、B2、B3、…Bn,连接A1B2、A2B3、A3B4、…、AnBn+1,设△OA1B1的面积为S1,△A1B1B2的面积为S2,△A1B2A2的面积为S3…,则S2015=( )
 如图,直线l1的解析式为y1=$\sqrt{3}$x,直线l2的解析式为y2=-$\frac{\sqrt{3}}{3}$x,过点(1,0)、(2,0)、(3,0)、(4,0)…(n,0)作y轴的平行线,与直线l1分别交于点A1、A2、A3、A4、…An,与直线l2分别交于点B1、B2、B3、…Bn,连接A1B2、A2B3、A3B4、…、AnBn+1,设△OA1B1的面积为S1,△A1B1B2的面积为S2,△A1B2A2的面积为S3…,则S2015=( )
如图,直线l1的解析式为y1=$\sqrt{3}$x,直线l2的解析式为y2=-$\frac{\sqrt{3}}{3}$x,过点(1,0)、(2,0)、(3,0)、(4,0)…(n,0)作y轴的平行线,与直线l1分别交于点A1、A2、A3、A4、…An,与直线l2分别交于点B1、B2、B3、…Bn,连接A1B2、A2B3、A3B4、…、AnBn+1,设△OA1B1的面积为S1,△A1B1B2的面积为S2,△A1B2A2的面积为S3…,则S2015=( )| A. | $\frac{2016\sqrt{3}}{3}$ | B. | 1008$\sqrt{3}$ | C. | $\frac{2015\sqrt{3}}{2}$ | D. | $\frac{2015\sqrt{3}}{3}$ |
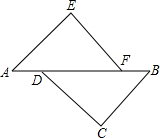 如图,AE∥BC,AE=BC,点D、F在AB上,且AD=BF.
如图,AE∥BC,AE=BC,点D、F在AB上,且AD=BF.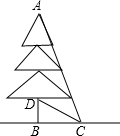 某小区在绿化改造项目中,要将一棵已经枯萎的树砍伐掉.在操作过程中,李师傅想直接从根部把树放倒,张师傅不同意,他担心这样会损坏这棵树周围10米处的花园和雕塑.通过测量知道图中∠BCD=30°,∠DCA=35°,BD=3米,根据计算说明张师傅的担心是否有必要?(结果精确到0.1位,tan65°≈2.1)
某小区在绿化改造项目中,要将一棵已经枯萎的树砍伐掉.在操作过程中,李师傅想直接从根部把树放倒,张师傅不同意,他担心这样会损坏这棵树周围10米处的花园和雕塑.通过测量知道图中∠BCD=30°,∠DCA=35°,BD=3米,根据计算说明张师傅的担心是否有必要?(结果精确到0.1位,tan65°≈2.1)