题目内容
12.已知抛物线y=x2+kx+k-1.(1)当k=3时,求抛物线与x轴的两个交点坐标;
(2)求证:无论k取任何实数,抛物线过x轴上一定点;
(3)设抛物线与y轴交于C点,与x轴交于A(xA,0),B(xB,0)两点,且满足:xA<xB<0,S△ABC=6,①求抛物线的表达式;②y轴负半轴上是否存在一点D,使得以A、C、D为顶点的三角形与△ABC相似?若存在,求出点D的坐标;若不存在,请说明理由.
分析 (1)把k=3代入y=x2+kx+k-1,得到y=x2+3x+2,令y=0,得x2+3x+2=0,再解方程求出x的值,即可求解;
(2)令x2+kx+k-1=0,解方程求得两根有一常数,问题得证;
(3)①由xA<xB<0,得1-k<0,分两种情况:
Ⅰ)若-1<1-k,则k<2,求得1<k<2,表示出AB、OC,代入S△ABC=6解答求k;
Ⅱ)若1-k<-1,则k>2,表示出AB、OC,代入S△ABC=6解答求k;
②由y=x2+5x+4求出A、B、C三点的坐标,进一步求得AB、AC,由△CAD∽△ABC,求出CD,得出OD,进而求出点D的坐标.
解答 (1)解:∵y=x2+kx+k-1,
∴当k=3时,y=x2+3x+2,
令y=0,得x2+3x+2=0,
解得x1=-1,x2=-2,
∴抛物线与x轴的交点坐标是(-1,0),(-2,0);
(2)证明:∵y=x2+kx+k-1,
∴当y=0时,x2+kx+k-1=0,
解得x1=-1,x2=1-k,
∴无论k取任何实数,抛物线过x轴上一定点(-1,0);
(3)解:①∵xA<xB<0,
∴1-k<0,即k>1.
分两种情况:
Ⅰ)若-1<1-k,则k<2,
∴1<k<2,这时xA=-1,xB=1-k,
∴AB=xB-xA=1-k-(-1)=2-k,且OC=k-1,
∴S△ABC=$\frac{1}{2}$(2-k)(k-1)=6,
整理,得k2-3k+14=0,
∵b2-4ac=(-3)2-4×14<0,
∴此方程无实数解,即-1<1-k不成立;
Ⅱ)若1-k<-1,则k>2,
∴这时xA=1-k,xB=-1,
∴AB=xB-xA=-1-(1-k)=k-2,且OC=k-1,
∴S△ABC=$\frac{1}{2}$(k-2)(k-1)=6,
整理,得(k-5)(k+2)=0, ∴k1=5,k2=-2(不合题意,舍去),
∴k1=5,k2=-2(不合题意,舍去),
∴所求抛物线的表达式为y=x2+5x+4;
②如图,存在一点D,使得以A、C、D为顶点的三角形与△ABC相似.
∵y=x2+5x+4,
∴A(-4,0),B(-1,0),C(0,4),
∴AB=3,OC=4,AC=4$\sqrt{2}$,
∵∠CAO=∠OCA=45°,
∴只有△CAD∽△ABC,
∴$\frac{CD}{AC}$=$\frac{AC}{AB}$,
∴CD=$\frac{A{C}^{2}}{AB}$=$\frac{32}{3}$,
∴OD=CD-OC=$\frac{32}{3}$-4=$\frac{20}{3}$,
∴D点坐标为(0,-$\frac{20}{3}$).
点评 本题是二次函数的综合题型,其中涉及到抛物线与x轴交点坐标的求法,二次函数解析式的确定、图形面积的求法、相似三角形的判定和性质等知识,渗透分类讨论及数形结合的思想.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案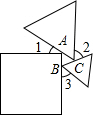 一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )
一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )| A. | 100° | B. | 120° | C. | 130° | D. | 180° |
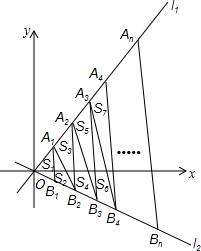 如图,直线l1的解析式为y1=$\sqrt{3}$x,直线l2的解析式为y2=-$\frac{\sqrt{3}}{3}$x,过点(1,0)、(2,0)、(3,0)、(4,0)…(n,0)作y轴的平行线,与直线l1分别交于点A1、A2、A3、A4、…An,与直线l2分别交于点B1、B2、B3、…Bn,连接A1B2、A2B3、A3B4、…、AnBn+1,设△OA1B1的面积为S1,△A1B1B2的面积为S2,△A1B2A2的面积为S3…,则S2015=( )
如图,直线l1的解析式为y1=$\sqrt{3}$x,直线l2的解析式为y2=-$\frac{\sqrt{3}}{3}$x,过点(1,0)、(2,0)、(3,0)、(4,0)…(n,0)作y轴的平行线,与直线l1分别交于点A1、A2、A3、A4、…An,与直线l2分别交于点B1、B2、B3、…Bn,连接A1B2、A2B3、A3B4、…、AnBn+1,设△OA1B1的面积为S1,△A1B1B2的面积为S2,△A1B2A2的面积为S3…,则S2015=( )| A. | $\frac{2016\sqrt{3}}{3}$ | B. | 1008$\sqrt{3}$ | C. | $\frac{2015\sqrt{3}}{2}$ | D. | $\frac{2015\sqrt{3}}{3}$ |
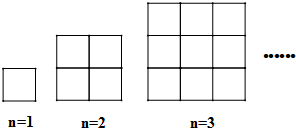
| A. | 220 | B. | 200 | C. | 120 | D. | 100 |
 如图,△ABC是边长为$\sqrt{3}$的等边三角形,点P.Q分别是射线AB、BC上两个动点,且AP=CQ,PQ交AC与D,作PE丄AC于E,那么DE的长度为$\frac{1}{2}$$\sqrt{3}$.
如图,△ABC是边长为$\sqrt{3}$的等边三角形,点P.Q分别是射线AB、BC上两个动点,且AP=CQ,PQ交AC与D,作PE丄AC于E,那么DE的长度为$\frac{1}{2}$$\sqrt{3}$.