题目内容
18.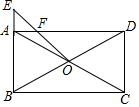 如图,在矩形ABCD中,对角线AC与BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F,若AB=6,BC=10,AE=2,求AF的长.
如图,在矩形ABCD中,对角线AC与BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F,若AB=6,BC=10,AE=2,求AF的长.
分析 如图,作OH⊥AD于H.设AF=x.首先证明OH是△ADB的中位线,推出OH=3,AE∥OH,得$\frac{AE}{OH}$=$\frac{AF}{FH}$,列出方程求解即可.
解答 解:如图,作OH⊥AD于H.设AF=x.
∵四边形ABCD是矩形,
∴∠BAD=90°=∠OHD,OB=OD,BC=AD=10,
∴OH∥AB,
∴AH=HD=5,OH=$\frac{1}{2}$AB=3,
∵AE∥OH,
∴$\frac{AE}{OH}$=$\frac{AF}{FH}$,
∴$\frac{2}{3}$=$\frac{x}{5-x}$,
∴x=2,
∴AF=2.
点评 本题考查矩形的性质、三角形的中位线定理、平行线分线段成比例定理等知识,解题的关键是学会添加常用辅助线,学会用方程的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
9.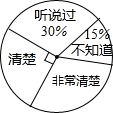 第十二届全国人大四次会议审议通过的《中华人民共和国慈善法》已于今年9月1日正式实施,为了了解居民对慈善法的知晓情况,某街道办从辖区居民中随机选取了900名居民进行调查,并将调查结果制作成了如下不完整的统计图和表:
第十二届全国人大四次会议审议通过的《中华人民共和国慈善法》已于今年9月1日正式实施,为了了解居民对慈善法的知晓情况,某街道办从辖区居民中随机选取了900名居民进行调查,并将调查结果制作成了如下不完整的统计图和表:
根据以上信息求得“非常清楚”所占扇形的百分比为30%.
 第十二届全国人大四次会议审议通过的《中华人民共和国慈善法》已于今年9月1日正式实施,为了了解居民对慈善法的知晓情况,某街道办从辖区居民中随机选取了900名居民进行调查,并将调查结果制作成了如下不完整的统计图和表:
第十二届全国人大四次会议审议通过的《中华人民共和国慈善法》已于今年9月1日正式实施,为了了解居民对慈善法的知晓情况,某街道办从辖区居民中随机选取了900名居民进行调查,并将调查结果制作成了如下不完整的统计图和表:| 听说过 | 不知道 | 清楚 | 非常清楚 |
| A | B | 225 | C |
10.若a=b,下列等式不一定成立的是( )
| A. | a-5=b-5 | B. | a+3=b+3 | C. | 2a=2b | D. | $\frac{a}{c}$=$\frac{b}{c}$ |
 先完成下列填空,再在同一直角坐标系中画出以下函数的图象(不必再列表)
先完成下列填空,再在同一直角坐标系中画出以下函数的图象(不必再列表)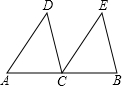 已知,如图,AC=BC,CD∥BE,且CD=BE.
已知,如图,AC=BC,CD∥BE,且CD=BE. 如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O相交于点D,求证:DE=DB.
如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O相交于点D,求证:DE=DB.