题目内容
7.已知关于x的一元二次方程x2-(m+1)x+$\frac{1}{4}$m2+$\frac{1}{2}$m-$\frac{3}{4}$=0的两根是一个矩形两邻边的长.(1)求矩形两邻边的长(用有关m的代数式表示);
(2)当矩形的对角线长为$\sqrt{10}$时,求m的值.
分析 (1)先求出△,再代入公式求出即可;
(2)根据勾股定理得出关于m的方程,求出方程的解即可.
解答 解:(1)x2-(m+1)x+$\frac{1}{4}$m2+$\frac{1}{2}$m-$\frac{3}{4}$=0,
x=$\frac{(m+1)±\sqrt{4}}{2}$,
x1=$\frac{m+3}{2}$,x2=$\frac{m-1}{2}$,
即矩形两邻边的长为$\frac{m+3}{2}$和$\frac{m-1}{2}$;
(2)∵矩形的对角线长为$\sqrt{10}$,
∴($\frac{m+3}{2}$)2+($\frac{m-1}{2}$)2=($\sqrt{10}$)2,
解得:m=-5或3,
当m=-5时,$\frac{m+3}{2}$=-1,边长不能为负数,不符合题意舍去,
所以m=3.
点评 本题考查了矩形的性质,勾股定理,根与系数的关系,根的判别式等知识点,能求出两边长是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
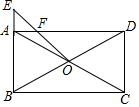 如图,在矩形ABCD中,对角线AC与BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F,若AB=6,BC=10,AE=2,求AF的长.
如图,在矩形ABCD中,对角线AC与BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F,若AB=6,BC=10,AE=2,求AF的长.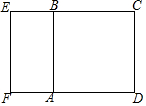 如图,现有一个边长是1的正方形ABCD,在它的左侧补一个矩形ABEF,使所得矩形CEFD∽矩形ABEF,求BE的长.
如图,现有一个边长是1的正方形ABCD,在它的左侧补一个矩形ABEF,使所得矩形CEFD∽矩形ABEF,求BE的长.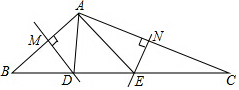 如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.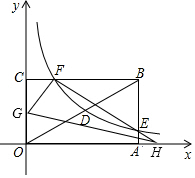 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,m)在边AB上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过点D、E,且cos∠BOA=$\frac{4}{5}$.
如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,m)在边AB上,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过点D、E,且cos∠BOA=$\frac{4}{5}$.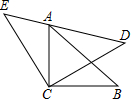 如图,△ACB和△ECD都是等腰直角三角形,CA=CA,CE=CD,△ACB的顶点A在△ECD的斜边DE上,求证:AE2+AD2=2AC2.(提示:连接BD)
如图,△ACB和△ECD都是等腰直角三角形,CA=CA,CE=CD,△ACB的顶点A在△ECD的斜边DE上,求证:AE2+AD2=2AC2.(提示:连接BD)