题目内容
8．
如图，点E是△ABC的内心，AE的延长线和△ABC的外接圆⊙O相交于点D，求证：DE=DB．
分析 根据内心的概念得到∠ABE=∠CBE，∠BAD=∠DBC，根据圆周角定理得到∠CAD=∠CAD，根据三角形的外角的性质、等腰三角形的判定定理证明即可．
解答 证明：∵点E是△ABC的内心，
∴∠ABE=∠CBE，∠BAD=∠DBC，
由圆周角定理得，∠CAD=∠CAD，
∴∠DBE=∠DBC+∠EBC=∠ABE+∠BAD=∠DEB，
∴DE=DB．
点评 本题考查的是三角形的内切圆和内心，掌握三角形的内心是三角形的三条角平分线的交点是解题的关键．
练习册系列答案
相关题目
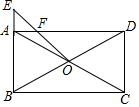如图，在矩形ABCD中，对角线AC与BD相交于点O，在BA的延长线上取一点E，连接OE交AD于点F，若AB=6，BC=10，AE=2，求AF的长．
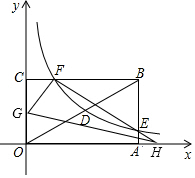如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点D为对角线OB的中点，点E（4，m）在边AB上，反比例函数y=$\frac{k}{x}$（k≠0）在第一象限内的图象经过点D、E，且cos∠BOA=$\frac{4}{5}$．
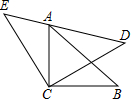如图，△ACB和△ECD都是等腰直角三角形，CA=CA，CE=CD，△ACB的顶点A在△ECD的斜边DE上，求证：AE2+AD2=2AC2．（提示：连接BD）
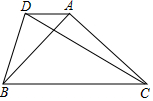如图，在△ABC中，∠BAC=90°，AB=AC，DA∥BC，tan∠DBA=$\frac{1}{2}$，若CD=2$\sqrt{17}$，则线段BC的长为，6$\sqrt{2}$．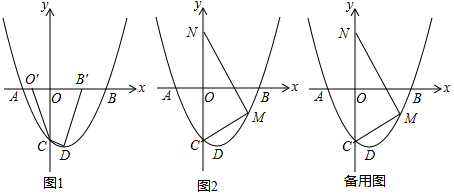
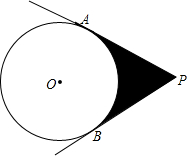如图，过⊙O外一点P向⊙O作两条切线，切点分别为A，B，若⊙O半径为2，∠APB=60°，则图中阴影部分的面积为4$\sqrt{3}$-$\frac{4}{3}$π．