题目内容
12.解方程组(或不等式组)(1)$\left\{\begin{array}{l}{3x+y=7}\\{5x-2y=8}\end{array}\right.$ (2)$\left\{\begin{array}{l}{5x-12≤2(4x-3)}\\{\frac{x+4}{2}<3-\frac{6x-1}{6}}\end{array}\right.$.
分析 (1)将①×2+②,消去y,解方程可得;
(2)分别求出每一个不等式的解集,根据口诀:大小小大中间找,可得不等式组的解集.
解答 解:(1)在方程组$\left\{\begin{array}{l}{3x+y=7}&{①}\\{5x-2y=8}&{②}\end{array}\right.$中,
①×2+②,得:11x=22,
解得:x=2,
将x=2代入①得:6+y=7,解得:y=1,
故方程组的解为:$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$;
(2)解不等式5x-12≤2(4x-3),得:x≥-2,
解不等式$\frac{x+4}{2}<3-\frac{6x-1}{6}$,得:x<$\frac{7}{9}$,
故不等式组解集为:-2≤x<$\frac{7}{9}$.
点评 本题主要考查解方程组和解一元一次不等式组的基本技能,熟练掌握消元的方法和解不等式的基本步骤是解题的关键.

练习册系列答案
相关题目
7.如果代数式$\frac{\sqrt{x}}{\sqrt{x-1}}$有意义,那么x的取值范围是( )
| A. | x≥0 | B. | x≠1 | C. | x>1 | D. | x≥0且 x≠1 |
 如图,在矩形ABCD中,E、F分别是AD、BC中点,连接AF、BE、CE、DF分别交于点M、N,四边形EMFN是菱形.
如图,在矩形ABCD中,E、F分别是AD、BC中点,连接AF、BE、CE、DF分别交于点M、N,四边形EMFN是菱形. 如图所示,在?ABCD中,BF⊥AD于F,BE⊥CD于E,若∠A=60°,AF=3cm,CE=2cm,则?ABCD的周长为20cm..
如图所示,在?ABCD中,BF⊥AD于F,BE⊥CD于E,若∠A=60°,AF=3cm,CE=2cm,则?ABCD的周长为20cm..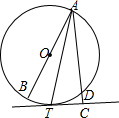 如图,AB是⊙O的直径,D是⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C
如图,AB是⊙O的直径,D是⊙O上一点,AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C