题目内容
17．
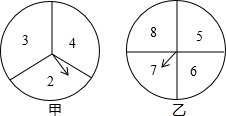如图两个可以自由转动的转盘，甲转盘被等分成3个扇形，乙转盘被等分成4个扇形，每一个扇形上都标有相应的数字，小亮和小颖利用它们做游戏，游戏规则是：同时转动两个转盘，当转盘停止后，指针所指区域内的数字之和小于10，小颖获胜；指针所指区域内的数字之和等于10，为平局；指针所指区域内的数字之和大于10，小亮获胜．如果指针恰好指在分割线上，那么重转一次，直到指针指向一个数字为止．（1）请你用列表法或树状图求小颖获胜的概率．
（2）你认为该游戏规则是否公平？请说明理由．
分析 （1）依据题意先用列表法或画树状图法分析所有等可能的出现结果，然后根据概率公式求出该事件的概率．
（2）判断游戏的公平性，首先要计算出游戏双方赢的概率，概率相等则公平，否则不公平．
解答 解：（1）共有12种等可能的结果，小于10的情况有6种，
所以指针所指区域内的数字和小于10的概率为$\frac{6}{12}$=$\frac{1}{2}$，
所以小颖获胜的概率是$\frac{3}{5}$；
| 和 | 2 | 3 | 4 |
| 6 | 8 | 9 | 10 |
| 7 | 9 | 10 | 11 |
| 8 | 10 | 11 | 12 |
| 5 | 7 | 8 | 9 |
小亮获胜的概率为$\frac{3}{12}$=$\frac{1}{4}$．小颖获胜的可能性大，
所以不公平．
点评 本题考查的是游戏公平性的判断．判断游戏公平性就要计算每个参与者取胜的概率，概率相等就公平，否则就不公平．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
12．已知正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象的一个交点坐标是（1，3），则另一个交点的坐标是（ ）
| A． | （-1，-3） | B． | （-3，-1） | C． | （-1，-2） | D． | （-2，-3） |
2．某股份有限公司根据公司实际情况，对本公司职工实行内部医疗公积金制度，公司规定：
（一）每位职工在年初需缴纳医疗公积金m元；
（二）职工个人当年治病花费的医疗费年底按表1的办法分段处理：
表1
设一职工当年治病花费的医疗费为x元，他个人实际承担的费用（包括医疗费中个人承担的部分和缴纳的医疗公积金m元）为y元．
（1）由表1可知，当0≤x≤150时，y=x+m；那么，当150＜x≤10000时，y与x的函数关系式（用含m、n的方式表示）为y=150+m+（x-150）n%（150＜x≤10000）．
（2）该公司职员小陈和大李2010年治病花费的医疗费和他们个人实际承担的费用如表2：
表2
请根据表2中的信息，求m、n的值，并求出当150＜x≤10000时，y关于x函数解析式；
（3）该公司职工个人一年因病实际承担费用最多只需要多少元？
（一）每位职工在年初需缴纳医疗公积金m元；
（二）职工个人当年治病花费的医疗费年底按表1的办法分段处理：
表1
| 分段方式 | 处理方法 |
| 不超过150元（含150元） | 全部由个人承担 |
| 超过150元，不超过10000元 （不含150元，含10000元）的部分 | 个人承担n%，剩余部分由公司承担 |
| 超过10000元（不含10000元）的部分 | 全部由公司承担 |
（1）由表1可知，当0≤x≤150时，y=x+m；那么，当150＜x≤10000时，y与x的函数关系式（用含m、n的方式表示）为y=150+m+（x-150）n%（150＜x≤10000）．
（2）该公司职员小陈和大李2010年治病花费的医疗费和他们个人实际承担的费用如表2：
表2
| 职工 | 治病花费的医疗费x（元） | 个人实际承担的费用y（元） |
| 小陈 | 300 | 280 |
| 大李 | 500 | 320 |
（3）该公司职工个人一年因病实际承担费用最多只需要多少元？
如图，平面直角坐标系中，点A的坐标是（4，0），点P在直线y=-x+m上，且AP=OP=4，那么m的值为2+2$\sqrt{3}$或2-2$\sqrt{3}$．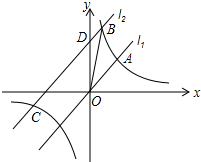
如图，直线l1：y=x与双曲线y=$\frac{k}{x}$相交于点A（3，a），将直线l1沿y轴向上平移8个单位单位得到l2，直线l2与双曲线相交于B、C两点（点B在第一象限），交y轴于D点．