题目内容
9. 如图,平面直角坐标系中,点A的坐标是(4,0),点P在直线y=-x+m上,且AP=OP=4,那么m的值为2+2$\sqrt{3}$或2-2$\sqrt{3}$.
如图,平面直角坐标系中,点A的坐标是(4,0),点P在直线y=-x+m上,且AP=OP=4,那么m的值为2+2$\sqrt{3}$或2-2$\sqrt{3}$.
分析 易知点P在线段OA的垂直平分线上,那么就能求得△AOP是等边三角形,就能求得点P的横坐标,根据勾股定理可求得点P的纵坐标.把这点代入一次函数解析式即可,同理可得到在第四象限的点.
解答  解:由已知AP=OP,点P在线段OA的垂直平分线PM上.
解:由已知AP=OP,点P在线段OA的垂直平分线PM上.
∴OA=AP=OP=4,
∴△AOP是等边三角形.
如图,当点P在第一象限时,OM=2,OP=4.
在Rt△OPM中,PM=$\sqrt{O{P}^{2}-O{M}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴P(2,2$\sqrt{3}$).
∵点P在y=-x+m上,
∴m=2+2$\sqrt{3}$.
当点P在第四象限时,根据对称性,P′(2,-2$\sqrt{3}$).
∵点P′在y=-x+m上,
∴m=2-2$\sqrt{3}$.
则m的值为2+2$\sqrt{3}$或2-2$\sqrt{3}$.
故答案为:2+2$\sqrt{3}$或2-2$\sqrt{3}$.
点评 此题主要考查了一次函数图象上点的坐标特征,解决本题的关键是求得点P的坐标,需注意点P的两种可能.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
19. 如图,已知△ABE≌△ACD,不正确的等式是( )
如图,已知△ABE≌△ACD,不正确的等式是( )
 如图,已知△ABE≌△ACD,不正确的等式是( )
如图,已知△ABE≌△ACD,不正确的等式是( )| A. | AB=AC | B. | ∠BAE=∠CAD | C. | AD=DE | D. | BE=DC |
20.某工厂计划生产A、B两种产品共60件,需购买甲、乙两种材料,生产一件A、B产品所需原料如表:
经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过9900元,且生产B产品不少于38件,问符合生产条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件A产品需加工费40元,若生产一件B产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低?(成本=材料费+加工费)
| 类别 | 甲种材料(千克) | 乙种材料(千克) |
| 1件A产品所需材料 | 4 | 1 |
| 1件B产品所需材料 | 3 | 3 |
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过9900元,且生产B产品不少于38件,问符合生产条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件A产品需加工费40元,若生产一件B产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低?(成本=材料费+加工费)
14.单项式-2x2y的系数和次数分别是( )
| A. | 2和2 | B. | -2和1 | C. | -2和3 | D. | -5和1 |
1.已知x2-$\frac{5}{3}$x的值是1,则3x2-5x+2014的值是( )
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
18.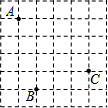 如图,在某个平面直角坐标系内,已知点A的坐标为(-3,2),点B的坐标为(-2,-2),则点C的坐标为( )
如图,在某个平面直角坐标系内,已知点A的坐标为(-3,2),点B的坐标为(-2,-2),则点C的坐标为( )
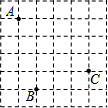 如图,在某个平面直角坐标系内,已知点A的坐标为(-3,2),点B的坐标为(-2,-2),则点C的坐标为( )
如图,在某个平面直角坐标系内,已知点A的坐标为(-3,2),点B的坐标为(-2,-2),则点C的坐标为( )| A. | (2,-3) | B. | (1,1) | C. | (-1,1) | D. | (1,-1) |
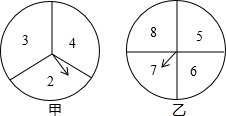 如图两个可以自由转动的转盘,甲转盘被等分成3个扇形,乙转盘被等分成4个扇形,每一个扇形上都标有相应的数字,小亮和小颖利用它们做游戏,游戏规则是:同时转动两个转盘,当转盘停止后,指针所指区域内的数字之和小于10,小颖获胜;指针所指区域内的数字之和等于10,为平局;指针所指区域内的数字之和大于10,小亮获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.
如图两个可以自由转动的转盘,甲转盘被等分成3个扇形,乙转盘被等分成4个扇形,每一个扇形上都标有相应的数字,小亮和小颖利用它们做游戏,游戏规则是:同时转动两个转盘,当转盘停止后,指针所指区域内的数字之和小于10,小颖获胜;指针所指区域内的数字之和等于10,为平局;指针所指区域内的数字之和大于10,小亮获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.