题目内容
8.一个正多边形中心角为60°,其外接圆的半径为2,其内切圆半径为$\sqrt{3}$.分析 首先确定中心角为60°的正多边形的边数,然后利用其边长求其外接圆的半径求出边长,由勾股定理求出内切圆半径即可.
解答 解:这个正多边形的边数:360°÷60°=6.
正六边形的半径与边长相等,
∴正六边形的边长=2,
如图所示:O为外接圆的圆心,
作OM⊥AB于M,连接OA,
则AM=$\frac{1}{2}$AB=1,
∴OM=$\sqrt{O{A}^{2}-A{M}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
即正六边形的内切圆半径为$\sqrt{3}$;
故答案为:$\sqrt{3}$.
点评 考查了正多边形和圆的知识、勾股定理;正六边形的半径与边长相等,是需要熟记的内容.

练习册系列答案
相关题目
19. 如图,已知△ABE≌△ACD,不正确的等式是( )
如图,已知△ABE≌△ACD,不正确的等式是( )
 如图,已知△ABE≌△ACD,不正确的等式是( )
如图,已知△ABE≌△ACD,不正确的等式是( )| A. | AB=AC | B. | ∠BAE=∠CAD | C. | AD=DE | D. | BE=DC |
16. 如图,在△ABC中,AC=1,BC=2,AB=$\sqrt{5}$,则cosB的值是( )
如图,在△ABC中,AC=1,BC=2,AB=$\sqrt{5}$,则cosB的值是( )
 如图,在△ABC中,AC=1,BC=2,AB=$\sqrt{5}$,则cosB的值是( )
如图,在△ABC中,AC=1,BC=2,AB=$\sqrt{5}$,则cosB的值是( )| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | 2 | D. | $\frac{1}{2}$ |
20.某工厂计划生产A、B两种产品共60件,需购买甲、乙两种材料,生产一件A、B产品所需原料如表:
经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过9900元,且生产B产品不少于38件,问符合生产条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件A产品需加工费40元,若生产一件B产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低?(成本=材料费+加工费)
| 类别 | 甲种材料(千克) | 乙种材料(千克) |
| 1件A产品所需材料 | 4 | 1 |
| 1件B产品所需材料 | 3 | 3 |
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过9900元,且生产B产品不少于38件,问符合生产条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件A产品需加工费40元,若生产一件B产品需加工费50元,应选择哪种生产方案,使生产这60件产品的成本最低?(成本=材料费+加工费)
18.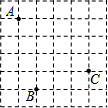 如图,在某个平面直角坐标系内,已知点A的坐标为(-3,2),点B的坐标为(-2,-2),则点C的坐标为( )
如图,在某个平面直角坐标系内,已知点A的坐标为(-3,2),点B的坐标为(-2,-2),则点C的坐标为( )
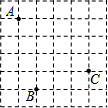 如图,在某个平面直角坐标系内,已知点A的坐标为(-3,2),点B的坐标为(-2,-2),则点C的坐标为( )
如图,在某个平面直角坐标系内,已知点A的坐标为(-3,2),点B的坐标为(-2,-2),则点C的坐标为( )| A. | (2,-3) | B. | (1,1) | C. | (-1,1) | D. | (1,-1) |

 如图,在矩形ABCD中,AB=1,(AD>AB)在BC上取一点E,沿AE将△ABE向上折叠,使点B落在AD上的点F,若四边形EFDC与原矩形相似,则AD的长度为$\frac{1+\sqrt{5}}{2}$.
如图,在矩形ABCD中,AB=1,(AD>AB)在BC上取一点E,沿AE将△ABE向上折叠,使点B落在AD上的点F,若四边形EFDC与原矩形相似,则AD的长度为$\frac{1+\sqrt{5}}{2}$.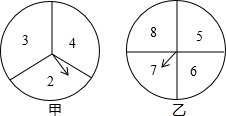 如图两个可以自由转动的转盘,甲转盘被等分成3个扇形,乙转盘被等分成4个扇形,每一个扇形上都标有相应的数字,小亮和小颖利用它们做游戏,游戏规则是:同时转动两个转盘,当转盘停止后,指针所指区域内的数字之和小于10,小颖获胜;指针所指区域内的数字之和等于10,为平局;指针所指区域内的数字之和大于10,小亮获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.
如图两个可以自由转动的转盘,甲转盘被等分成3个扇形,乙转盘被等分成4个扇形,每一个扇形上都标有相应的数字,小亮和小颖利用它们做游戏,游戏规则是:同时转动两个转盘,当转盘停止后,指针所指区域内的数字之和小于10,小颖获胜;指针所指区域内的数字之和等于10,为平局;指针所指区域内的数字之和大于10,小亮获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.