题目内容

7．已知二次函数的顶点坐标为（-1，-4），与y轴的交点坐标为（0，-2）．
①求抛物线的表达式；
②写出函数值y为负数时，自变量x的取值范围．

分析 （1）根据顶点坐标可设抛物线的表达式为：y=a（x+1）2-4，将（0，-2）代入求出a的值即可；
（2）根据题意y＜0，可得不等式，解不等式即可．

解答 解：（1）设抛物线的表达式为：y=a（x+1）2-4，
将（0，-2）代入得，a-4=-2，
解得：a=2，
故抛物线表达式为：y=2（x+1）2-4；
（2）当y＜0时，即2（x+1）2-4＜0，
解得：-$\sqrt{2}$-1＜x＜$\sqrt{2}$-1．

点评 本题主要考查二次函数解析式的求法及二次函数性质，根据顶点坐标设其顶点式是关键．

练习册系列答案
相关题目
7．两人练习百米跑步，甲的成绩（单位：s）为13、12、14、12、12；乙的成绩为12、11、13、14、12．问谁的成绩好一些？谁的成绩稳定一些？
18．一座奖杯主视图如图所示，底座上部轮廓是抛物线的一部分，如图，包装奖杯的包装盒是-个长、宽都为a（cm），高为b（cm）的长方体纸盒．长方体纸盒侧面ABCD周长为120cm，长方体表面积为S（cm2）．
（1）试用只含a的代数式表示S；
（2）若2a≤b，当a取何值时，S有最大值，求出S的最大值；
（3）图3是把奖杯放入包装盒后的剖面图，FG=a（cm），GH=b（cm），底座宽度较小能放入盒中，以FG所在直线为x轴，以FG中垂线为y轴建立平面直角坐标系，抛物线的解析式为y=mx2+10，a取（2）中使S最大的a的值，若奖杯高度等于包装盒的高度b（cm），抛物线过（8，26）．试判断奖杯能否放进包装盒并说明理由．
15．已知31=3，32=9，33=27，34=81，35=243，36=729，37=2187，…，请你推测32016的个位数字是（　　）
A．3B．9C．7D．1
2．将抛物线y=2x2-1向下平移3个单位后，所得抛物线的表达式是y=2x2-4．
12．（1）尝试探究：“如图1，在□ABCD中，点E是BC边上的中点，点G是射线CD上一点（点G不与点C重合），BG交AE于点F，若$\frac{AF}{EF}$=$\frac{5}{2}$，求$\frac{CG}{CD}$的值．”在解决这一问题时，我们可以过点E作EH∥AB交BG于点H，则AB和EH的数量关系是AB=$\frac{5}{2}$EH，CG和EH的数量关系是CG=2EH，$\frac{CG}{CD}$的值是$\frac{4}{5}$；
（2）类比延伸：如图2，在□ABCD中，点E是BC边上的点（点E不与B、C两点重合），点G是射线CD上一点（点G不与点C重合），BG交AE于点F，若$\frac{AF}{EF}$=m，$\frac{BE}{EC}$=n，求$\frac{CG}{CD}$的值；（用含m、n的代数式表示，写出解答过程）
（3）应用迁移：在□ABCD中，点E是BC边上的点（点E不与B、C两点重合），点G是射线CD上一点（点G不与点C重合），BG交AE于点F，若$\frac{AF}{EF}$=$\frac{35}{18}$，$\frac{DG}{CD}$=$\frac{2}{7}$，则$\frac{BE}{EC}$的值为$\frac{2}{3}$或$\frac{18}{7}$．
19．如图，已知△ABE≌△ACD，不正确的等式是（　　）
A．AB=ACB．∠BAE=∠CADC．AD=DED．BE=DC
16．如图，在△ABC中，AC=1，BC=2，AB=$\sqrt{5}$，则cosB的值是（　　）
A．$\frac{2\sqrt{5}}{5}$B．$\frac{\sqrt{5}}{5}$C．2D．$\frac{1}{2}$
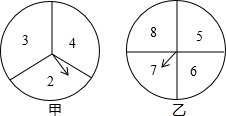17．如图两个可以自由转动的转盘，甲转盘被等分成3个扇形，乙转盘被等分成4个扇形，每一个扇形上都标有相应的数字，小亮和小颖利用它们做游戏，游戏规则是：同时转动两个转盘，当转盘停止后，指针所指区域内的数字之和小于10，小颖获胜；指针所指区域内的数字之和等于10，为平局；指针所指区域内的数字之和大于10，小亮获胜．如果指针恰好指在分割线上，那么重转一次，直到指针指向一个数字为止．
（1）请你用列表法或树状图求小颖获胜的概率．
（2）你认为该游戏规则是否公平？请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网