题目内容
9.在函数y=$\frac{1-2x}{x-2}$中,自变量x的取值范围是x≠2.分析 根据分式的意义有意义的条件:分母不等于0,可以求出x的范围.
解答 解:根据题意得:x-2≠0,
解得x≠2.
故答案是:x≠2.
点评 本题考查了函数自变量的取值范围,函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.

练习册系列答案
相关题目
4.已知⊙O1与⊙O2的半径分别为3cm和4cm,O1O2=6cm,则两圆的位置关系为( )
| A. | 内切 | B. | 相交 | C. | 外切 | D. | 外离 |
14.下列代数运算正确的是( )
| A. | (x2)3=x5 | B. | (2x)3=2x3 | C. | x•x3=x4 | D. | (x-1)2=x2-1 |
19.不等式3x≤x+m的正整数解只有2个,则m的取值范围是( )
| A. | 4<m<6 | B. | 4≤m≤6 | C. | 4≤m<6 | D. | 4<m≤6 |
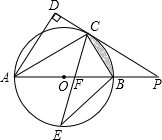 如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为D,直线DC与AB的延长线交于点P,弦CE平分∠ACB,交AB于点F,连结BE,BE=7$\sqrt{2}$.下列四个结论:①AC平分∠DAB;②PF2=PB•PA;③若BC=$\frac{1}{2}$OP,则阴影部分的面积为$\frac{7}{4}$π-$\frac{49}{4}$$\sqrt{3}$;④若PC=24,则tan∠PCB=$\frac{3}{4}$.其中正确的是( )
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为D,直线DC与AB的延长线交于点P,弦CE平分∠ACB,交AB于点F,连结BE,BE=7$\sqrt{2}$.下列四个结论:①AC平分∠DAB;②PF2=PB•PA;③若BC=$\frac{1}{2}$OP,则阴影部分的面积为$\frac{7}{4}$π-$\frac{49}{4}$$\sqrt{3}$;④若PC=24,则tan∠PCB=$\frac{3}{4}$.其中正确的是( )