��Ŀ����
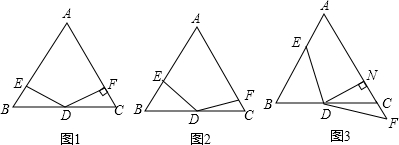
17���ڡ�ABC�У�AB=AC����A=60�㣬��D���߶�BC���е㣬��EDF=120�㣬DE���߶�AB�ཻ�ڵ�E��DF���߶�AC����AC���ӳ��ߣ��ཻ�ڵ�F����1����ͼ1����DF��AC������ΪF��AB=8����BE�ij���
��2����ͼ2������1���еġ�EDF�Ƶ�D˳ʱ����תһ���ĽǶȣ�DF�����߶�AC�ཻ�ڵ�F����֤��BE+CF=$\frac{1}{2}$AB��
��3����ͼ3������2���еġ�EDF�����Ƶ�D˳ʱ����תһ���ĽǶȣ�ʹDF���߶�AC���ӳ����ཻ�ڵ�F����DN��AC�ڵ�N����DN=FN��AB=8����BE�ij���
���� ��1����ͼ1������á�B=60�㣬��BED=90�㣬BD=4��Ȼ���������Ǻ����Ķ���Ϳ����BE��ֵ��
��2������D��DM��AB��M����DN��AC��N����ͼ2����֤��MBD�ա�NCD������BM=CN��DM=DN��������֤����EMD�ա�FND������EM=FN���Ϳɵõ�BE+CF=BM+EM+CF=BM+FN+CF=BM+CN=2BM=2BD��cos60��=BD=$\frac{1}{2}$BC=$\frac{1}{2}$AB��
��3������D��DM��AB��M����ͼ3��ͬ��1���ɵã���B=��ACD=60�㣬ͬ��2���ɵã�BM=CN��DM=DN��EM=FN����DN=FN�ɵ�DM=DN=FN=EM���Ӷ��ɵ�BE+CF=BM+EM+CF=CN+DM+CF=NF+DM=2DM=2BD��sin60��=$\frac{\sqrt{3}}{2}$BC=$\frac{\sqrt{3}}{2}$AB����ΪBE+CF=BE+NF-CN=BE+DM-BM=BE+$\frac{\sqrt{3}}{2}$BD-$\frac{1}{2}$BD=$\frac{\sqrt{3}}{2}$AB����AB=8��BD=4���뼴�ɵõ�BE=2$\sqrt{3}$+2��
��� �⣺��1����ͼ1��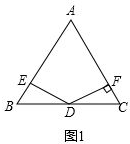
��AB=AC����A=60�㣬
���ABC�ǵȱ������Σ�
���B=��C=60�㣬BC=AC=AB=4��
�ߵ�D���߶�BC���е㣬
��BD=DC=$\frac{1}{2}$BC=4��
��DF��AC������AFD=90�㣬
���AED=360��-60��-90��-120��=90�㣬
���BED=90�㣬
��BE=BD��cos��B=4��cos60��=4��$\frac{1}{2}$=2��
��2������D��DM��AB��M����DN��AC��N����ͼ2��
���С�AMD=��BMD=��AND=��CND=90�㣮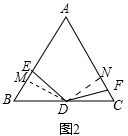
�ߡ�A=60�㣬���MDN=360��-60��-90��-90��=120�㣮
�ߡ�EDF=120�㣬���MDE=��NDF��
�ڡ�MBD�͡�NCD�У�$\left\{\begin{array}{l}{��BMD=��CND}\\{��B=��C}\\{BD=CD}\end{array}\right.$��
���MBD�ա�NCD��
��BM=CN��DM=DN��
�ڡ�EMD�͡�FND�У�$\left\{\begin{array}{l}{��EMD=��FND}\\{DM=DN}\\{��MDE=��NDF}\end{array}\right.$��
���EMD�ա�FND��
��EM=FN��
��BE+CF=BM+EM+CF=BM+FN+CF=BM+CN
=2BM=2BD��cos60��=BD=$\frac{1}{2}$BC=$\frac{1}{2}$AB��
��3������D��DM��AB��M����ͼ3��
ͬ��1���ɵã���B=��ACD=60�㣮
ͬ��2���ɵã�BM=CN��DM=DN��EM=FN��
��DN=FN��
��DM=DN=FN=EM��
��BE+CF=BM+EM+CF=CN+DM+CF=NF+DM=2DM=2BD��sin60��=$\frac{\sqrt{3}}{2}$BC=$\frac{\sqrt{3}}{2}$AB��
�ࣨ2���еĽ��۲�������
��AB=8��
��BD=4��
��BE+CF=BE+NF-CN=BE+DM-BM=BE+$\frac{\sqrt{3}}{2}$BD-$\frac{1}{2}$BD=$\frac{\sqrt{3}}{2}$AB��
��BE=2$\sqrt{3}$+2��
���� ������Ҫ�����˵ȱ������ε��ж������ʡ��ı��ε��ڽǺͶ�����ȫ�������ε��ж������ʡ����Ǻ����Ķ��塢����ǵ����Ǻ���ֵ��֪ʶ��ͨ��֤��������ȫ�ȵõ�BM=CN��DM=DN��EM=FN�ǽ������Ĺؼ���

 �ٷ�ѧ����ҵ��������ϵ�д�
�ٷ�ѧ����ҵ��������ϵ�д� ��������ϵ�д�
��������ϵ�д� ��ͼ���ƻ�Χһ�����Ϊ50m2�ij����γ��أ�һ�߿���ǽ��ǽ��Ϊ10m�����������������Χ�ɣ��������ij����֮��Ϊ5��2�����۷���ʱ��СӢ˵�������Dz�����Χ������Ҫ��ij����γ��أ���С��˵��������ͳ���������ȷ���ģ��϶�����Χ�ó������������ж�˭��˵����ȷ��Ϊʲô��
��ͼ���ƻ�Χһ�����Ϊ50m2�ij����γ��أ�һ�߿���ǽ��ǽ��Ϊ10m�����������������Χ�ɣ��������ij����֮��Ϊ5��2�����۷���ʱ��СӢ˵�������Dz�����Χ������Ҫ��ij����γ��أ���С��˵��������ͳ���������ȷ���ģ��϶�����Χ�ó������������ж�˭��˵����ȷ��Ϊʲô�� ��ͼ��ij�칫¥AB�ĺ�����һ������CD�������������ļн���22��ʱ���칫¥�ڽ������ǽ�����¸�22��Ӱ��CE���������������н���45��ʱ���칫¥��A�ڵ����ϵ�Ӱ��F��ǽ��C��25�ľ��루B��F��C��һ��ֱ���ϣ���
��ͼ��ij�칫¥AB�ĺ�����һ������CD�������������ļн���22��ʱ���칫¥�ڽ������ǽ�����¸�22��Ӱ��CE���������������н���45��ʱ���칫¥��A�ڵ����ϵ�Ӱ��F��ǽ��C��25�ľ��루B��F��C��һ��ֱ���ϣ���
 ��ͼ����ֱ֪��l����A��ֱ��l��һ�㣬�ó߹���l�Ĵ��ߣ�ʹ��������A��������ͼ�ۼ�����д������
��ͼ����ֱ֪��l����A��ֱ��l��һ�㣬�ó߹���l�Ĵ��ߣ�ʹ��������A��������ͼ�ۼ�����д������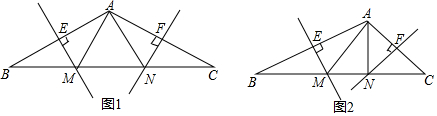
 ��ͼ��AE��BF��ACƽ�֡�BAE����BF��C��
��ͼ��AE��BF��ACƽ�֡�BAE����BF��C��