题目内容
已知直线L外有两点A B,AC⊥L BD⊥L,垂足分别为C、D,且AC=3,BD=8.CD=12,当A、B在L同侧时,在L上求一点P使PA+PB值最小,画出图形,并求出最小值.
考点:轴对称-最短路线问题
专题:
分析:以直线L为轴作A点对称点A′,连接A′B交直线l于P,则A′B就是PA+PB最小值;根据勾股定理求得A′B的长,即可求得PA+PB的最小值.
解答: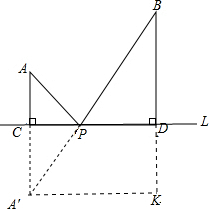 解:作A点关于直线L的对称点A′,连接A′B交直线L于P,则PA+PB=A′P+BP=A′B,A′B就是PA+PB的最小值;
解:作A点关于直线L的对称点A′,连接A′B交直线L于P,则PA+PB=A′P+BP=A′B,A′B就是PA+PB的最小值;
延长BD使KD=A′C,连接A′K,
∵AC⊥L BD⊥L,
∴AA′∥BK,
∴四边形A′KDC是矩形,
∴KD=AC=3,A′K=CD=12,
∴BK=BD+KD=8+3=11,
∴A′B=
=
,
∴PA+PB最小值为
.
 解:作A点关于直线L的对称点A′,连接A′B交直线L于P,则PA+PB=A′P+BP=A′B,A′B就是PA+PB的最小值;
解:作A点关于直线L的对称点A′,连接A′B交直线L于P,则PA+PB=A′P+BP=A′B,A′B就是PA+PB的最小值;延长BD使KD=A′C,连接A′K,
∵AC⊥L BD⊥L,
∴AA′∥BK,
∴四边形A′KDC是矩形,
∴KD=AC=3,A′K=CD=12,
∴BK=BD+KD=8+3=11,
∴A′B=
| 122+112 |
| 265 |
∴PA+PB最小值为
| 265 |
点评:本题考查了轴对称-最短路线问题,应用的知识点有:轴对称的性质,矩形的判定和性质,勾股定理的应用等,作出直角三角形是关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
 如图,AB=CD,AD=BC,O为BD上任意一点,过O点的直线分别交AD、BC于M、N两点.求证:∠1=∠2.
如图,AB=CD,AD=BC,O为BD上任意一点,过O点的直线分别交AD、BC于M、N两点.求证:∠1=∠2. 如图,两个同心圆的半径分别为2cm和4cm,有大圆上一点A作小圆的两条切线AB、AC,切点为B、C,求图中阴影部分的面积.
如图,两个同心圆的半径分别为2cm和4cm,有大圆上一点A作小圆的两条切线AB、AC,切点为B、C,求图中阴影部分的面积. 如图,在正方形ABCD中,F是AD边的中点,E是BA延长线上一点,且AE=
如图,在正方形ABCD中,F是AD边的中点,E是BA延长线上一点,且AE=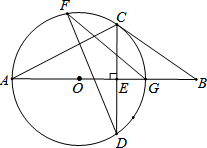 如图,AG为⊙O的直径,弦CD⊥AG,垂足为E,F为⊙O上点,B为AG延长线上点.
如图,AG为⊙O的直径,弦CD⊥AG,垂足为E,F为⊙O上点,B为AG延长线上点.