题目内容
20．当x满足-5＜x≤3时，$\frac{1-3x}{2}$的值不小于-4且小于8．分析 先根据题意得出关于x的不等式组，求出x的取值范围即可．
解答 解：∵$\frac{1-3x}{2}$的值不小于-4且小于8，
∴$\left\{\begin{array}{l}\frac{1-3x}{2}≥-4①\\ \frac{1-3x}{2}＜8②\end{array}\right.$，由①得，x≤3，由②得，x＞-5，
故不等式组的解集为：-5＜x≤3．
点评 本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
赢在课堂名师课时计划系列答案
相关题目
10．一个平行四边形的两条对角线的长分别为8和10，则这个平行四边形边长不可能是（ ）
| A． | 2 | B． | 5 | C． | 8 | D． | 10 |
11．下列各式是最简二次根式的是（ ）
| A． | $\sqrt{5{x}^{2}}$ | B． | $\sqrt{0.9}$ | C． | $\sqrt{\frac{3}{7}}$ | D． | $\sqrt{{a}^{2}-3}$ |
5．下列计算正确的是（ ）
| A． | $\sqrt{3}+\sqrt{2}=\sqrt{5}$ | B． | $3\sqrt{2}-2\sqrt{2}=1$ | C． | $\sqrt{3^2}=3$ | D． | $\sqrt{9}=±3$ |
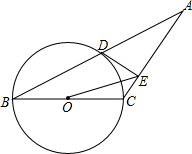如图，在△ABC中，以BC为直径的⊙O与底边AB交于点D，过D作DE⊥AC，垂足为E．