题目内容
11.下列各式是最简二次根式的是( )| A. | $\sqrt{5{x}^{2}}$ | B. | $\sqrt{0.9}$ | C. | $\sqrt{\frac{3}{7}}$ | D. | $\sqrt{{a}^{2}-3}$ |
分析 先根据二次根式的性质化简,再根据最简二次根式的定义判断即可.
解答 解:A、$\sqrt{5{x}^{2}}=|x|\sqrt{5}$,故不是最简二次根式,故A选项错误;
B、$\sqrt{0.9}=\frac{3}{10}\sqrt{10}$,故不是最简二次根式,故B选项错误;
C、$\sqrt{\frac{3}{7}}=\frac{\sqrt{21}}{7}$,故不是最简二次根式,故C选项错误;
D、不能化简,是最简二次根式,故D选项正确;
故选D,.
点评 本题考查了对最简二次根式的定义的理解,能理解最简二次根式的定义是解此题的关键.

练习册系列答案
相关题目
2.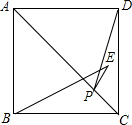 如图,E是正方形ABCD内一点,BA=BE,P是对角线AC上的一点,若AC=$\sqrt{2}$,则PE+PD的最小值为( )
如图,E是正方形ABCD内一点,BA=BE,P是对角线AC上的一点,若AC=$\sqrt{2}$,则PE+PD的最小值为( )
 如图,E是正方形ABCD内一点,BA=BE,P是对角线AC上的一点,若AC=$\sqrt{2}$,则PE+PD的最小值为( )
如图,E是正方形ABCD内一点,BA=BE,P是对角线AC上的一点,若AC=$\sqrt{2}$,则PE+PD的最小值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
16.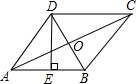 如图,菱形ABCD的周长为40cm,对角线AC、BD相交于点O,DE⊥AB,垂足为E,DE:AB=4:5,则下列结论:①DE=8cm;②BE=4cm;③BD=4$\sqrt{5}$cm;④AC=8$\sqrt{5}$cm;⑤S菱形ABCD=80cm,正确的有( )
如图,菱形ABCD的周长为40cm,对角线AC、BD相交于点O,DE⊥AB,垂足为E,DE:AB=4:5,则下列结论:①DE=8cm;②BE=4cm;③BD=4$\sqrt{5}$cm;④AC=8$\sqrt{5}$cm;⑤S菱形ABCD=80cm,正确的有( )
 如图,菱形ABCD的周长为40cm,对角线AC、BD相交于点O,DE⊥AB,垂足为E,DE:AB=4:5,则下列结论:①DE=8cm;②BE=4cm;③BD=4$\sqrt{5}$cm;④AC=8$\sqrt{5}$cm;⑤S菱形ABCD=80cm,正确的有( )
如图,菱形ABCD的周长为40cm,对角线AC、BD相交于点O,DE⊥AB,垂足为E,DE:AB=4:5,则下列结论:①DE=8cm;②BE=4cm;③BD=4$\sqrt{5}$cm;④AC=8$\sqrt{5}$cm;⑤S菱形ABCD=80cm,正确的有( )| A. | ①②④⑤ | B. | ①②③④ | C. | ①③④⑤ | D. | ①②③④⑤ |
1.光明文具厂工人的工作时间:每月26天,每天8小时.待遇:按件计酬,多劳多得,每月另加福利工资920元,按月结算.该厂生产A,B两种型号零件,工人每生产一件A种型号零件,可得报酬0.85元,每生产一件B种型号零件,可得报酬1.5元,下表记录的是工人小王的工作情况:
根据上表提供的信息,请回答如下问题:
(1)小王每生产一件A种型号零件、每生产一件B种型号零件,分别需要多少分钟?
(2)设小王某月生产A种型号零件x件,该月工资为y元,求y与x的函数关系式;
(3)如果生产两种型号零件的数目无限制,那么小王该月的工资数目最多为多少?
| 生产A种型号零件/件 | 生产B种型号零件/件 | 总时间/分 |
| 2 | 2 | 70 |
| 6 | 4 | 170 |
(1)小王每生产一件A种型号零件、每生产一件B种型号零件,分别需要多少分钟?
(2)设小王某月生产A种型号零件x件,该月工资为y元,求y与x的函数关系式;
(3)如果生产两种型号零件的数目无限制,那么小王该月的工资数目最多为多少?
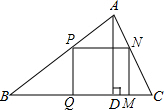 如图,△ABC是一块锐角三角形余料,边BC=12cm,高AD=8cm,要把它加工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上.若这个矩形的长是宽的2倍,求矩形的长和宽.
如图,△ABC是一块锐角三角形余料,边BC=12cm,高AD=8cm,要把它加工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上.若这个矩形的长是宽的2倍,求矩形的长和宽.