题目内容
 在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,折痕DF交BC于点F.
在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,折痕DF交BC于点F.(1)求证:四边形BFDE为平行四边形;
(2)若AB=6cm,BC=8cm,求线段NF的长.
考点:翻折变换(折叠问题)
专题:
分析:(1)利用矩形性质得出∠ABE=∠CDF,∠EBD=∠FDB,进而得出△ABE≌△CDF,即可得出EB∥DF,EB=DF,即可得出答案;
(2)根据翻折变换的性质设NF=xcm,则FC=xcm,BF=(8-x)cm,CD=DN=6cm,则BN=10-6=4(cm),进而利用勾股定理求出NF的长.
(2)根据翻折变换的性质设NF=xcm,则FC=xcm,BF=(8-x)cm,CD=DN=6cm,则BN=10-6=4(cm),进而利用勾股定理求出NF的长.
解答: (1)证明:∵四边形ABCD为矩形,
(1)证明:∵四边形ABCD为矩形,
∴AB∥CD,AB=CD,∠A=∠C.
∴∠ABD=∠CDB,
由翻折知,∠ABE=∠EBD=
∠ABD,∠CDF=∠FDB=
∠CDB,
∴∠ABE=∠CDF,∠EBD=∠FDB,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(ASA),
∴EB=DF,
∵∠EBD=∠FDB,
∴EB∥DF,
∴四边形EBFD为平行四边形;
(2)解:∵AB=6cm,BC=8cm,
∴BD=
=10(cm),
∴设NF=xcm,则FC=xcm,BF=(8-x)cm,CD=DN=6cm,则BN=10-6=4(cm),
在Rt△BNF中,BN2+NF2=BF2,
∴42+x2=(8-x)2,
解得:x=3,
故线段NF的长为3cm.
 (1)证明:∵四边形ABCD为矩形,
(1)证明:∵四边形ABCD为矩形,∴AB∥CD,AB=CD,∠A=∠C.
∴∠ABD=∠CDB,
由翻折知,∠ABE=∠EBD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ABE=∠CDF,∠EBD=∠FDB,
在△ABE和△CDF中,
|
∴△ABE≌△CDF(ASA),
∴EB=DF,
∵∠EBD=∠FDB,
∴EB∥DF,
∴四边形EBFD为平行四边形;
(2)解:∵AB=6cm,BC=8cm,
∴BD=
| 62+82 |
∴设NF=xcm,则FC=xcm,BF=(8-x)cm,CD=DN=6cm,则BN=10-6=4(cm),
在Rt△BNF中,BN2+NF2=BF2,
∴42+x2=(8-x)2,
解得:x=3,
故线段NF的长为3cm.
点评:此题主要考查了矩形的性质以及全等三角形的判定与性质和平行四边形的判定以及勾股定理等知识,根据已知得出△ABE≌△CDF是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知:∠A=∠D,AC∥FD,AC=FD,求证:FB=CE.
如图,已知:∠A=∠D,AC∥FD,AC=FD,求证:FB=CE.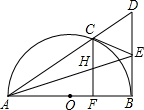 已知:C是以AB为直径的半圆O上一点,CF⊥AB于点F,直线AC与过B点的切线相交于点D,E为BD中点,连接AE交CF于点H,连接CE.
已知:C是以AB为直径的半圆O上一点,CF⊥AB于点F,直线AC与过B点的切线相交于点D,E为BD中点,连接AE交CF于点H,连接CE. 四边形ABCD是平行四边形,且AB=BE,CD=DF.
四边形ABCD是平行四边形,且AB=BE,CD=DF.