题目内容
 如图,梯形ABCD中,AD∥BC,AD=3,BC=7,E、F分别是AB、CD的中点,G在BC上,EG∥AF,则CG的长等于
如图,梯形ABCD中,AD∥BC,AD=3,BC=7,E、F分别是AB、CD的中点,G在BC上,EG∥AF,则CG的长等于考点:三角形中位线定理,全等三角形的判定与性质
专题:
分析:延长AF、BC相交于点H,利用“角边角”证明△ADF和△HCF全等,根据全等三角形对应边相等可得CH=AD,然后求出BH,再求出EG是△ABH的中位线,然后求出BG,再根据CG=BC-BG计算即可得解.
解答: 解:如图,延长AF、BC相交于点H,
解:如图,延长AF、BC相交于点H,
∵点F是CD的中点,
∴CF=DF,
∵AD∥BC,
∴∠D=∠FCH,
在△ADF和△HCF中,
,
∴△ADF≌△HCF(ASA),
∴CH=AD=3,
∴BH=BC+CH=7+3=10,
∵点E是AB的中点,EG∥AF,
∴EG是△ABH的中位线,
∴BG=
BH=
×10=5,
∴CG=BC-BG=7-5=2.
故答案为:2.
 解:如图,延长AF、BC相交于点H,
解:如图,延长AF、BC相交于点H,∵点F是CD的中点,
∴CF=DF,
∵AD∥BC,
∴∠D=∠FCH,
在△ADF和△HCF中,
|
∴△ADF≌△HCF(ASA),
∴CH=AD=3,
∴BH=BC+CH=7+3=10,
∵点E是AB的中点,EG∥AF,
∴EG是△ABH的中位线,
∴BG=
| 1 |
| 2 |
| 1 |
| 2 |
∴CG=BC-BG=7-5=2.
故答案为:2.
点评:本题考查了三角形的中位线,全等三角形的判定与性质,作辅助线构造成全等三角形并判断出EG是△ABH的中位线是解题的关键.

练习册系列答案
相关题目
 如图,⊙A的圆心A的坐标是(2,3),x轴与⊙A相切于点D,与y轴交于B,C两点,则cos∠ABC为( )
如图,⊙A的圆心A的坐标是(2,3),x轴与⊙A相切于点D,与y轴交于B,C两点,则cos∠ABC为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
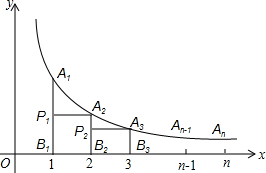 如图,在反比例函数y=
如图,在反比例函数y= 如图,a∥b,点A在直线a上,点C在直线b上,∠BAC=90°,AB=AC,若∠1=20°,则∠2的度数为
如图,a∥b,点A在直线a上,点C在直线b上,∠BAC=90°,AB=AC,若∠1=20°,则∠2的度数为