题目内容
“中华紫薇园”景区今年“五一”期间开始营业,为方便游客在园区内游玩休息,决定向一家园艺公司采购一批户外休闲椅,经了解,公司出售两种型号休闲椅,如下表:
景区采购这批休闲椅共用去56000元,购得的椅子正好可让1300名游客同时使用.
(1)求景区采购了多少条长条椅,多少条弧形椅?
(2)景区现计划租用A、B两种型号的卡车共20辆将这批椅子运回景区,已知A型卡车每辆可同时装运4条长条椅和11条弧形椅,B型卡车每辆可同时装运12条长条椅和7条弧形椅.如何安排A、B两种卡车可一次性将这批休闲椅运回来?
(3)又知A型卡车每辆的运费为1200元,B型卡车每辆的运费为1050元,在(2)的条件下,若要使此次运费最少,应采取哪种方案?并求出最少的运费为多少元.
| 可供使用人数(人/条) | 价格(元/条) | |
| 长条椅 | 3 | 160 |
| 弧形椅 | 5 | 200 |
(1)求景区采购了多少条长条椅,多少条弧形椅?
(2)景区现计划租用A、B两种型号的卡车共20辆将这批椅子运回景区,已知A型卡车每辆可同时装运4条长条椅和11条弧形椅,B型卡车每辆可同时装运12条长条椅和7条弧形椅.如何安排A、B两种卡车可一次性将这批休闲椅运回来?
(3)又知A型卡车每辆的运费为1200元,B型卡车每辆的运费为1050元,在(2)的条件下,若要使此次运费最少,应采取哪种方案?并求出最少的运费为多少元.
考点:一次函数的应用,二元一次方程组的应用,一元一次不等式组的应用
专题:
分析:(1)设景区采购长条椅x条,弧型椅y条,然后根据游客人数和花费钱数两个等量关系列出方程组求解即可;
(2)设租用A型卡车m辆,则租用B种卡车(20-m)辆,根据两种型号卡车装运的休闲椅的数量不小于两种休闲椅的数量列出不等式组,求解即可,再根据车辆数是正整数写出设计方案;
(3)设租车总费用为W元,列出W的表达式,再根据一次函数的增减性求出最少费用.
(2)设租用A型卡车m辆,则租用B种卡车(20-m)辆,根据两种型号卡车装运的休闲椅的数量不小于两种休闲椅的数量列出不等式组,求解即可,再根据车辆数是正整数写出设计方案;
(3)设租车总费用为W元,列出W的表达式,再根据一次函数的增减性求出最少费用.
解答:解:(1)设景区采购长条椅x条,弧型椅y条,
由题意得,
,
解得
.
答:采购了100条长条椅,200条弧型椅;
(2)设租用A型卡车m辆,则租用B种卡车(20-m)辆,
由题意得
,
解得15≤m≤17.5,
由题意可知,m为正整数,
所以,m只能取15、16、17,
故有三种租车方案可一次性将这批休闲椅运回来,可这样安排:
方案一:A型卡车15辆,B型卡车5辆,
方案二:A型卡车16辆,B型卡车4辆,
方案三:A型卡车17辆,B型卡车3辆;
(3)设租车总费用为W元,则W=1200m+1050(20-m)=150m+21000,
∵150>0,
∴W随m的增大而增大,
又∵15≤m≤17.5,
∴当m=15时,W有最小值,W最小=150×15+21000=23250,
∴最省钱的租车方案是租用A型卡车15辆、B型卡车5辆,最低运费为23250元.
由题意得,
|
解得
|
答:采购了100条长条椅,200条弧型椅;
(2)设租用A型卡车m辆,则租用B种卡车(20-m)辆,
由题意得
|
解得15≤m≤17.5,
由题意可知,m为正整数,
所以,m只能取15、16、17,
故有三种租车方案可一次性将这批休闲椅运回来,可这样安排:
方案一:A型卡车15辆,B型卡车5辆,
方案二:A型卡车16辆,B型卡车4辆,
方案三:A型卡车17辆,B型卡车3辆;
(3)设租车总费用为W元,则W=1200m+1050(20-m)=150m+21000,
∵150>0,
∴W随m的增大而增大,
又∵15≤m≤17.5,
∴当m=15时,W有最小值,W最小=150×15+21000=23250,
∴最省钱的租车方案是租用A型卡车15辆、B型卡车5辆,最低运费为23250元.
点评:本题考查了一次函数的应用,二元一次方程组的应用,一元一次不等式组的应用,读懂题目信息,理解数量关系并确定出等量关系和不等量关系是解题的关键,(3)利用一次函数的增减性和自变量的取值范围求最值是常用的方法.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
下列运算正确的是( )
| A、a+a=a2 |
| B、a3•a4=a12 |
| C、(a2b)3=a6b3 |
| D、a3÷a4=a(a≠0) |
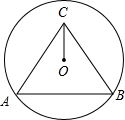 如图,圆O过点B、C,圆心O在正△ABC的内部,AB=2
如图,圆O过点B、C,圆心O在正△ABC的内部,AB=2| 3 |
A、
| ||
| B、2 | ||
C、
| ||
D、
|
下列运算正确的是( )
| A、x3•x2=x6 |
| B、(x2)3=x5 |
| C、2a-3a=-a |
| D、(x-2)2=x2+4 |
 如图,梯形ABCD中,AD∥BC,AD=3,BC=7,E、F分别是AB、CD的中点,G在BC上,EG∥AF,则CG的长等于
如图,梯形ABCD中,AD∥BC,AD=3,BC=7,E、F分别是AB、CD的中点,G在BC上,EG∥AF,则CG的长等于
