题目内容
如图，某水平地面上建筑物的高度为AB，在点D和点F处分别竖立高是2米的标杆CD和EF，两标杆相隔52米，并且建筑物AB、标杆CD和EF在同一竖直平面内，从标杆CD后退2米到点G处，在G处测得建筑物顶端A和标杆顶端C在同一条直线上；从标杆FE后退4米到点H处，在H处测得建筑物顶端A和标杆顶端E在同一条直线上，则建筑物的高是考点：相似三角形的应用
专题：几何图形问题,压轴题
分析：根据题意可得出△CDG∽△ABG，△EFH∽△ABH，再根据相似三角形的对应边成比例即可得出结论．
解答：解：∵AB⊥BH，CD⊥BH，EF⊥BH，
∴AB∥CD∥EF，
∴△CDG∽△ABG，△EFH∽△ABH，
∴
=
，
=
，
∵CD=DG=EF=2m，DF=52m，FH=4m，
∴
=
，
=
，
∴
=
，
解得BD=52m，
∴
=
，
解得AB=54m．
故答案为：54．
∴AB∥CD∥EF，
∴△CDG∽△ABG，△EFH∽△ABH，
∴
| CD |
| AB |
| DG |
| DG+BD |
| EF |
| AB |
| FH |
| FH+DF+BD |
∵CD=DG=EF=2m，DF=52m，FH=4m，
∴
| 2 |
| AB |
| 2 |
| 2+BD |
| 2 |
| AB |
| 4 |
| 4+52+BD |
∴
| 2 |
| 2+BD |
| 4 |
| 4+52+BD |
解得BD=52m，
∴
| 2 |
| AB |
| 2 |
| 2+52 |
解得AB=54m．
故答案为：54．
点评：本题考查的是相似三角形的应用，熟知相似三角形的对应边成比例是解答此题的关键．
练习册系列答案
七星图书口算速算天天练系列答案
相关题目
如图，抛物线y=ax2+bx+c（a＞0）的对称轴是过点（1，0）且平行于y轴的直线，若点P（4，0）在该抛物线上，则4a-2b+c的值为
如图，在?ABCD中，F是BC上的一点，直线DF与AB的延长线相交于点E，BP∥DF，且与AD相交于点P，请从图中找出一组相似的三角形：
如图，在△ABC中，AB=AC=5，BC=8．若∠BPC=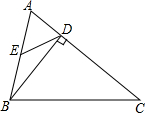
如图，在锐角△ABC中，点E为AB的中点，BD⊥AC于点D，若AC=20，CD=15，tanC=
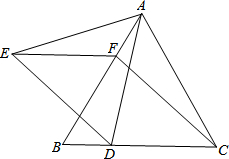如图，等边△ABC中，D、F分别是边BC、AB上的点，且CD=BF，以AD为边向左作等边△ADE，连接CF、EF，设BD：DC=K．