题目内容

若
243n
是一个整数，则整数n的最小值是
 
．
考点：二次根式的定义
专题：
分析：因为
243n
是整数，且
243n
=
81×3n
=9
3n
，则3n是完全平方数，满足条件的最小正整数n为3．
解答：解：∵
243n
=
81×3n
=9
3n
，且
243n
是整数；
∴9
3n
是整数，即3n是完全平方数；
∴n的最小正整数值为3．
故答案为：3．
点评：主要考查了乘除法法则和二次根式有意义的条件．二次根式有意义的条件是被开方数是非负数．二次根式的运算法则：乘法法则
a
•
b
=
ab
．除法法则
b
a
=
b
a
．解题关键是分解成一个完全平方数和一个代数式的积的形式．
练习册系列答案
相关题目
小武新家装修，在装修客厅时，购进彩色地砖和单色地砖共100块，共花费5600元．已知彩色地砖的单价是80元/块，单色地砖的单价是40元/块．
（1）两种型号的地砖各采购了多少块？
（2）如果厨房也要铺设这两种型号的地砖共60块，且采购地砖的费用不超过3200元，那么彩色地砖最多能采购多少块？
如图，在△ABC中，∠ABC=90°，D是边AC上的一点，连接BD，使∠A=2∠1，E是BC上的一点，以BE为直径的⊙O经过点D．
（1）求证：AC是⊙O的切线；
（2）若∠A=60°，⊙O的半径为2，求阴影部分的面积．（结果保留根号和π）
计算：2x3÷x=
 
．
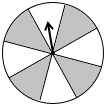有一个能自由转动的转盘如图，盘面被分成8个大小与性状都相同的扇形，颜色分为黑白两种，将指针的位置固定，让转盘自由转动，当它停止后，指针指向白色扇形的概率是
 
．
计算：82014×（-0.125）2015=
 
．
如图，某水平地面上建筑物的高度为AB，在点D和点F处分别竖立高是2米的标杆CD和EF，两标杆相隔52米，并且建筑物AB、标杆CD和EF在同一竖直平面内，从标杆CD后退2米到点G处，在G处测得建筑物顶端A和标杆顶端C在同一条直线上；从标杆FE后退4米到点H处，在H处测得建筑物顶端A和标杆顶端E在同一条直线上，则建筑物的高是
 
米．
如图，在等腰△ABC中，AB=AC，∠A=36°，BD⊥AC于点D，则∠CBD=
 
．
反比例函数y=-
2
x
（x＞0），点B为其上一点，点A为x轴负半轴上一点，当点B的横坐标逐渐减小时，△AOB的面积（　　）
A、逐渐减少B、逐渐增大
C、不变D、先增大后减小

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网