题目内容
如图，抛物线y=ax2+bx+c（a＞0）的对称轴是过点（1，0）且平行于y轴的直线，若点P（4，0）在该抛物线上，则4a-2b+c的值为考点：抛物线与x轴的交点
专题：数形结合
分析：依据抛物线的对称性求得与x轴的另一个交点，代入解析式即可．
解答：
解：设抛物线与x轴的另一个交点是Q，
∵抛物线的对称轴是过点（1，0），与x轴的一个交点是P（4，0），
∴与x轴的另一个交点Q（-2，0），
把（-2，0）代入解析式得：0=4a-2b+c，
∴4a-2b+c=0，
故答案为：0．
解：设抛物线与x轴的另一个交点是Q，∵抛物线的对称轴是过点（1，0），与x轴的一个交点是P（4，0），
∴与x轴的另一个交点Q（-2，0），
把（-2，0）代入解析式得：0=4a-2b+c，
∴4a-2b+c=0，
故答案为：0．
点评：本题考查了抛物线的对称性，知道与x轴的一个交点和对称轴，能够表示出与x轴的另一个交点，求得另一个交点坐标是本题的关键．
练习册系列答案
期末集结号系列答案
相关题目
如图，在△ABC中，∠ABC=90°，D是边AC上的一点，连接BD，使∠A=2∠1，E是BC上的一点，以BE为直径的⊙O经过点D．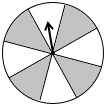
有一个能自由转动的转盘如图，盘面被分成8个大小与性状都相同的扇形，颜色分为黑白两种，将指针的位置固定，让转盘自由转动，当它停止后，指针指向白色扇形的概率是
如图，某水平地面上建筑物的高度为AB，在点D和点F处分别竖立高是2米的标杆CD和EF，两标杆相隔52米，并且建筑物AB、标杆CD和EF在同一竖直平面内，从标杆CD后退2米到点G处，在G处测得建筑物顶端A和标杆顶端C在同一条直线上；从标杆FE后退4米到点H处，在H处测得建筑物顶端A和标杆顶端E在同一条直线上，则建筑物的高是
如图，在Rt△ABC中，M、N是两直角边上的点，且AM=BC，CM=BN，BM、AN交于点P，则∠APM的度数为