题目内容
5.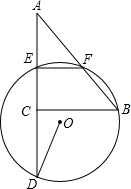 如图,△ABC中,AC=3,BC=4,∠ACB=90°,E、F分别为AC、AB的中点,过E、F两点作⊙O,延长AC交⊙O于D.若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )
如图,△ABC中,AC=3,BC=4,∠ACB=90°,E、F分别为AC、AB的中点,过E、F两点作⊙O,延长AC交⊙O于D.若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | $\sqrt{10}$ | D. | $\frac{7}{2}$ |
分析 连接OF交BC于G,连接OE,证明BG=BF═$\frac{5}{2}$,CG=$\frac{3}{2}$,根据EF∥BC,得到$\frac{CD}{DE}$=$\frac{CG}{EF}$,求出CD的长,根据勾股定理求出直径DF,得到半径.
解答 解:连接OF交BC于G,连接OE,
∵E、F分别为AC、AB的中点,∴EF∥BC,EF=$\frac{1}{2}$BC=2,EC=$\frac{1}{2}$AC=$\frac{3}{2}$,
∵OE=OF,∴∠OEF=∠OFE,
∵EF∥BC,
∴∠DEF=∠DCB=90°,
∴DF为直径,
∴∠BGF=∠OFE,
∵∠D=$\frac{1}{2}$∠EOF,∠CDO=$\frac{1}{2}$∠B,
∴∠EOF=∠B,
∴∠OEF=∠BFG,
∴∠BGF=∠BFG,
∴BG=BF=$\frac{5}{2}$,CG=$\frac{3}{2}$,
∵EF∥BC,
∴$\frac{CD}{DE}$=$\frac{CG}{EF}$,
∴CD=3CE=$\frac{9}{2}$,
在Rt△DFE中,EF=2,DE=6,
DF=2$\sqrt{10}$,OD=$\sqrt{10}$.
故选:C.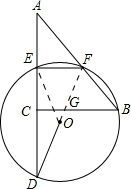
点评 本题考查的是三角形中位线定理、勾股定理、圆周角与圆心角的关系定理,正确作出辅助线、构造等腰三角形是解题的关键,注意平行线分线段成比例定理的应用.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
14.如果正三角形的内切圆半径为1,那么这个正三角形的边长为( )
| A. | 2 | B. | 2$\sqrt{3}$ | C. | 3 | D. | $\sqrt{3}$ |
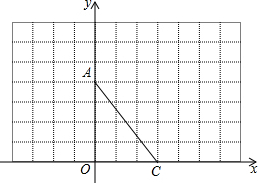 如图,在直角坐标系中,A(0,4),C(3,0).
如图,在直角坐标系中,A(0,4),C(3,0).