题目内容
15.有三套内容完全相同的古典小说,其中有两套是2014年出版的,有一套是2015年出版的,且每套书分上、下两册,每册书的外形都没有区别,现在将这6册书打乱后随机摆放在书架上,然后再从中任意取出2册.(1)用列表画树形图的方法表示所有可能的结果;
(2)求这2册书恰好是上、下两册的概率;
(3)求这2册书恰好是同一年出版的概率.
分析 (1)首先分别用A,B,C,a,b,c六本书,A,B,C表示上册,a,b,c表示下册,然后根据题意画出树状图,再由树状图求得所有等可能的结果;
(2)由(1)可求得这2册书恰好是上、下两册的情况,再利用概率公式即可求得答案;
(3)由(1)可求得这2册书恰好是同一年出版的情况,再利用概率公式即可求得答案.
解答 解:(1)分别用A,B,C,a,b,c六本书,A,B,C表示上册,a,b,c表示下册,
画树状图得:
则共有30种等可能的结果;
(2)∵这2册书恰好是上、下两册的有6种情况,
∴这2册书恰好是上、下两册的概率为:$\frac{6}{30}$=$\frac{1}{5}$;
(3)∵这2册书恰好是同一年出版的有14种情况,
∴这2册书恰好是同一年出版的概率为:$\frac{14}{30}$=$\frac{7}{15}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.如图所示,∠2和∠1是对顶角的是( )
| A. |  | B. |  | C. |  | D. |  |
3.要使式子$\frac{{\sqrt{x-1}}}{x}$有意义,x的取值范围是( )
| A. | x≠1 | B. | x≠0 | C. | x>1且x≠0 | D. | x≥1 |
20.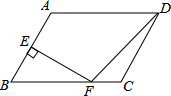 在?ABCD中,AB=6,AD=8,∠ABC=60°,点E是AB的中点,EF⊥AB交BC于F,连接DF,则DF的长为( )
在?ABCD中,AB=6,AD=8,∠ABC=60°,点E是AB的中点,EF⊥AB交BC于F,连接DF,则DF的长为( )
 在?ABCD中,AB=6,AD=8,∠ABC=60°,点E是AB的中点,EF⊥AB交BC于F,连接DF,则DF的长为( )
在?ABCD中,AB=6,AD=8,∠ABC=60°,点E是AB的中点,EF⊥AB交BC于F,连接DF,则DF的长为( )| A. | 2$\sqrt{13}$ | B. | 8 | C. | 5$\sqrt{2}$ | D. | 10 |
5.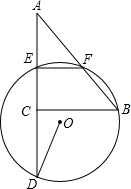 如图,△ABC中,AC=3,BC=4,∠ACB=90°,E、F分别为AC、AB的中点,过E、F两点作⊙O,延长AC交⊙O于D.若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )
如图,△ABC中,AC=3,BC=4,∠ACB=90°,E、F分别为AC、AB的中点,过E、F两点作⊙O,延长AC交⊙O于D.若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )
 如图,△ABC中,AC=3,BC=4,∠ACB=90°,E、F分别为AC、AB的中点,过E、F两点作⊙O,延长AC交⊙O于D.若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )
如图,△ABC中,AC=3,BC=4,∠ACB=90°,E、F分别为AC、AB的中点,过E、F两点作⊙O,延长AC交⊙O于D.若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | $\sqrt{10}$ | D. | $\frac{7}{2}$ |
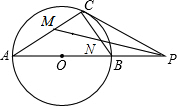 如图,已知⊙O为△ABC的外接圆,AB为⊙O直径,点P为线段AB延长线上一点,连接PC,∠CAB=∠BCP,PM为∠CPB的角平分线,交AC于点M,交BC于点N
如图,已知⊙O为△ABC的外接圆,AB为⊙O直径,点P为线段AB延长线上一点,连接PC,∠CAB=∠BCP,PM为∠CPB的角平分线,交AC于点M,交BC于点N