题目内容
14.如果正三角形的内切圆半径为1,那么这个正三角形的边长为( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 3 | D. | $\sqrt{3}$ |
分析 欲求三角形的边长,已知内切圆半径,可过内心向正三角形的一边作垂线,连接顶点与内切圆心,构造直角三角形求解.
解答  解:过O点作OD⊥AB,则OD=1.
解:过O点作OD⊥AB,则OD=1.
∵O是△ABC的内心,
∴∠OAD=30°;
Rt△OAD中,∠OAD=30°,OD=1,
∴AD=$\frac{OD}{tan30°}$=$\sqrt{3}$,
∴AB=2AD=2$\sqrt{3}$.
故选B.
点评 本题主要考查等边三角形的性质、三角形内切圆的性质,关键在于作辅助线构建直角三角形.

练习册系列答案
相关题目
5.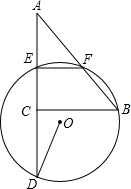 如图,△ABC中,AC=3,BC=4,∠ACB=90°,E、F分别为AC、AB的中点,过E、F两点作⊙O,延长AC交⊙O于D.若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )
如图,△ABC中,AC=3,BC=4,∠ACB=90°,E、F分别为AC、AB的中点,过E、F两点作⊙O,延长AC交⊙O于D.若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )
 如图,△ABC中,AC=3,BC=4,∠ACB=90°,E、F分别为AC、AB的中点,过E、F两点作⊙O,延长AC交⊙O于D.若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )
如图,△ABC中,AC=3,BC=4,∠ACB=90°,E、F分别为AC、AB的中点,过E、F两点作⊙O,延长AC交⊙O于D.若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | $\sqrt{10}$ | D. | $\frac{7}{2}$ |
9. 如图,在?ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC交BC边于点E,则BE等于( )
如图,在?ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC交BC边于点E,则BE等于( )
 如图,在?ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC交BC边于点E,则BE等于( )
如图,在?ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC交BC边于点E,则BE等于( )| A. | $\sqrt{2}$cm | B. | 2cm | C. | 3cm | D. | 4cm |
19.下面的几何体中,俯视图为三角形的是( )
| A. |  | B. |  | C. |  | D. |  |
6. 如图,一张矩形纸片ABCD的长AB=a,宽BC=b.将纸片对折,折痕为EF,所得矩形AFED与矩形ABCD相似,则a:b=( )
如图,一张矩形纸片ABCD的长AB=a,宽BC=b.将纸片对折,折痕为EF,所得矩形AFED与矩形ABCD相似,则a:b=( )
 如图,一张矩形纸片ABCD的长AB=a,宽BC=b.将纸片对折,折痕为EF,所得矩形AFED与矩形ABCD相似,则a:b=( )
如图,一张矩形纸片ABCD的长AB=a,宽BC=b.将纸片对折,折痕为EF,所得矩形AFED与矩形ABCD相似,则a:b=( )| A. | 2:1 | B. | $\sqrt{2}$:1 | C. | 3:$\sqrt{3}$ | D. | 3:2 |
3.下列运算中正确的是( )
| A. | x+x3=x4 | B. | x•x3=x4 | C. | (x2)3=x5 | D. | x6÷x3=x2 |
4.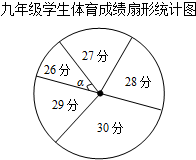 为了解某校九年级学生体育模考情况,现从中随机抽取部分学生的体育模考成绩统计如下,其中扇形统计图中的圆心角α为36°.
为了解某校九年级学生体育模考情况,现从中随机抽取部分学生的体育模考成绩统计如下,其中扇形统计图中的圆心角α为36°.
根据上面提供的信息,回答下列问题:
(1)m=10;抽取的部分学生体育模考成绩的中位数为29;
(2)已知该校九年级共有500名学生,如果体育模考成绩达29分(含29分)为优秀,请估计该校九年级学生体育模考成绩达到优秀的总人数.
 为了解某校九年级学生体育模考情况,现从中随机抽取部分学生的体育模考成绩统计如下,其中扇形统计图中的圆心角α为36°.
为了解某校九年级学生体育模考情况,现从中随机抽取部分学生的体育模考成绩统计如下,其中扇形统计图中的圆心角α为36°.| 九年级学生体育模考成绩统计表 | ||
| 体育成绩(分) | 人数(人) | 百分比(%) |
| 26 | 5 | 10 |
| 27 | m | 20 |
| 28 | 8 | 16 |
| 29 | 12 | 24 |
| 30 | 15 | |
(1)m=10;抽取的部分学生体育模考成绩的中位数为29;
(2)已知该校九年级共有500名学生,如果体育模考成绩达29分(含29分)为优秀,请估计该校九年级学生体育模考成绩达到优秀的总人数.