题目内容
16.$\sqrt{8}$-$\sqrt{2}$=$\sqrt{2}$;(3$\sqrt{5}$)2=45;$\sqrt{6y}$÷$\sqrt{\frac{2}{y}}$=$\sqrt{3}$y.分析 分别根据二次根式的加减法则及乘除法则进行计算即可.
解答 解:$\sqrt{8}$-$\sqrt{2}$=2$\sqrt{2}$-$\sqrt{2}$=$\sqrt{2}$;
(3$\sqrt{5}$)2=45;
$\sqrt{6y}$÷$\sqrt{\frac{2}{y}}$=$\sqrt{6y•\frac{y}{2}}$=$\sqrt{3{y}^{2}}$=$\sqrt{3}$y.
故答案为:$\sqrt{2}$,45,$\sqrt{3}$y.
点评 本题考查的是二次根式的乘除法,熟知二次根式的乘除法则是解答此题的关键.

练习册系列答案
相关题目
6.如图所示,∠2和∠1是对顶角的是( )
| A. |  | B. |  | C. |  | D. |  |
11.下列语句中不是命题的是( )
| A. | 有理数的混合运算 | B. | 对顶角相等 | ||
| C. | 若∠1=∠2,∠2=∠3,则∠1=∠3 | D. | 任何数的平方都是非负数 |
8. 如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,A处受噪音影响的时间为( )
如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,A处受噪音影响的时间为( )
 如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,A处受噪音影响的时间为( )
如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,A处受噪音影响的时间为( )| A. | 12秒 | B. | 16秒 | C. | 20秒 | D. | 30秒. |
5.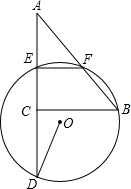 如图,△ABC中,AC=3,BC=4,∠ACB=90°,E、F分别为AC、AB的中点,过E、F两点作⊙O,延长AC交⊙O于D.若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )
如图,△ABC中,AC=3,BC=4,∠ACB=90°,E、F分别为AC、AB的中点,过E、F两点作⊙O,延长AC交⊙O于D.若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )
 如图,△ABC中,AC=3,BC=4,∠ACB=90°,E、F分别为AC、AB的中点,过E、F两点作⊙O,延长AC交⊙O于D.若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )
如图,△ABC中,AC=3,BC=4,∠ACB=90°,E、F分别为AC、AB的中点,过E、F两点作⊙O,延长AC交⊙O于D.若∠CDO=$\frac{1}{2}$∠B,则⊙O的半径为( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | $\sqrt{10}$ | D. | $\frac{7}{2}$ |
6. 如图,一张矩形纸片ABCD的长AB=a,宽BC=b.将纸片对折,折痕为EF,所得矩形AFED与矩形ABCD相似,则a:b=( )
如图,一张矩形纸片ABCD的长AB=a,宽BC=b.将纸片对折,折痕为EF,所得矩形AFED与矩形ABCD相似,则a:b=( )
 如图,一张矩形纸片ABCD的长AB=a,宽BC=b.将纸片对折,折痕为EF,所得矩形AFED与矩形ABCD相似,则a:b=( )
如图,一张矩形纸片ABCD的长AB=a,宽BC=b.将纸片对折,折痕为EF,所得矩形AFED与矩形ABCD相似,则a:b=( )| A. | 2:1 | B. | $\sqrt{2}$:1 | C. | 3:$\sqrt{3}$ | D. | 3:2 |
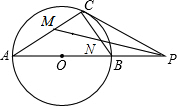 如图,已知⊙O为△ABC的外接圆,AB为⊙O直径,点P为线段AB延长线上一点,连接PC,∠CAB=∠BCP,PM为∠CPB的角平分线,交AC于点M,交BC于点N
如图,已知⊙O为△ABC的外接圆,AB为⊙O直径,点P为线段AB延长线上一点,连接PC,∠CAB=∠BCP,PM为∠CPB的角平分线,交AC于点M,交BC于点N