题目内容
16.若一元二次方程x2-ax+4=0有两个不相等的实数根,则a的值可以是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据一元二次方程x2-ax+4=0有两个不相等的实数根,可知一元二次方程根的判别式△>0,据此求出a的取值范围,进而求解即可.
解答 解:∵一元二次方程x2-ax+4=0有两个不相等的实数根,
∴△>0,
∴(-a)2-4×4>0,
∴a2>16,
∴a>4或a<-4.
故选D.
点评 此题考查了根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;
③当△<0时,方程无实数根.上面的结论反过来也成立.

练习册系列答案
相关题目
1.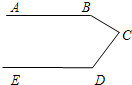 如图,一环湖公路的AB段为东西方向,经过三次拐弯后,又变成了东西方向的ED段,则∠B+∠C+∠D的度数为( )
如图,一环湖公路的AB段为东西方向,经过三次拐弯后,又变成了东西方向的ED段,则∠B+∠C+∠D的度数为( )
 如图,一环湖公路的AB段为东西方向,经过三次拐弯后,又变成了东西方向的ED段,则∠B+∠C+∠D的度数为( )
如图,一环湖公路的AB段为东西方向,经过三次拐弯后,又变成了东西方向的ED段,则∠B+∠C+∠D的度数为( )| A. | 180° | B. | 270° | C. | 360° | D. | 450° |
5.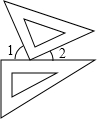 一副三角板按如图方式摆放,且∠1的度数比∠2的度数大44°,则∠1=( )
一副三角板按如图方式摆放,且∠1的度数比∠2的度数大44°,则∠1=( )
 一副三角板按如图方式摆放,且∠1的度数比∠2的度数大44°,则∠1=( )
一副三角板按如图方式摆放,且∠1的度数比∠2的度数大44°,则∠1=( )| A. | 18° | B. | 54° | C. | 67° | D. | 72° |
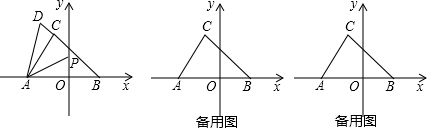
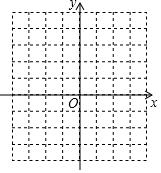 已知函数y1=x2-2x-3.
已知函数y1=x2-2x-3.