题目内容
11.设二次函数f(x)=ax2+bx有f(x1-1)=f(x2+1),x1-x2≠2,则f(x1+x2)=0.分析 由f(x1-1)=f(x2+1),x1-x2≠2,可得a(x1+x2)+b=0,而f(x1+x2)=a(x1+x2)2+b(x1+x2)=(x1+x2)[a(x1+x2)+b],从而求得答案.
解答 解:∵f(x1-1)=f(x2+1),
∴a(x1-1)2+b(x1-1)=a(x2+1)2+b(x2+1),
化为(x1-x2-2)[a(x1+x2)+b]=0,
∵x1-x2≠2,
∴a(x1+x2)+b=0,
∴f(x1+x2)=a(x1+x2)2+b(x1+x2)=(x1+x2)[a(x1+x2)+b]=0.
故答案为0.
点评 本题本题考查了二次函数点性质、函数值的计算问题,熟练、正确计算是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.若一元二次方程x2-ax+4=0有两个不相等的实数根,则a的值可以是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
1.直线y=(3-π)x经过的象限是( )
| A. | 一、二象限 | B. | 一、三象限 | C. | 二、三象限 | D. | 二、四象限 |

 如图,在矩形ABCD中,AB=4,BC=3,点P是矩形ABCD内的一个动点,且∠APB=90°,连接PC,若PC的长为整数,则PC的长可能为2或3或4.
如图,在矩形ABCD中,AB=4,BC=3,点P是矩形ABCD内的一个动点,且∠APB=90°,连接PC,若PC的长为整数,则PC的长可能为2或3或4.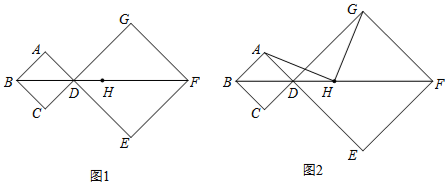
 如图是一束平行的阳光从教室窗户射入的平面示意图,小强同学测量出BC=1m,
如图是一束平行的阳光从教室窗户射入的平面示意图,小强同学测量出BC=1m,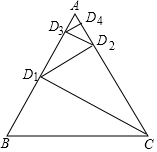 某同学用一等边三角形木板制作一些相似的直角三角形.如图,其方法是:过C点作CD1⊥AB于D1,再过D1作D1D2⊥CA于D2,再过D2作D2D3⊥AB于D3…,若△ABC的边长为a,则CD1=$\frac{\sqrt{3}}{2}$a,D1D2=$\frac{\sqrt{3}}{4}$a,D2D3=$\frac{\sqrt{3}}{8}$a,依此规律,则D5D6的长为$\frac{\sqrt{3}}{64}$a.
某同学用一等边三角形木板制作一些相似的直角三角形.如图,其方法是:过C点作CD1⊥AB于D1,再过D1作D1D2⊥CA于D2,再过D2作D2D3⊥AB于D3…,若△ABC的边长为a,则CD1=$\frac{\sqrt{3}}{2}$a,D1D2=$\frac{\sqrt{3}}{4}$a,D2D3=$\frac{\sqrt{3}}{8}$a,依此规律,则D5D6的长为$\frac{\sqrt{3}}{64}$a. 已知,如图,正方形ABCD的边长为12,菱形EFGH的三个顶点E,G,H分别在正方形ABCD的边AB,CD,DA上,AH=4,连接CF.
已知,如图,正方形ABCD的边长为12,菱形EFGH的三个顶点E,G,H分别在正方形ABCD的边AB,CD,DA上,AH=4,连接CF.