题目内容
1．若m是关于x的方程x2-2x-8=0的一个根，则2016-2m2+4m=2000．分析 根据一元二次方程的解的定义，将x=m代入已知方程，即可求得（m2-2m）的值，然后将其整体代入所求的代数式进行求值即可．
解答 解：依题意得：m2-2m-8=0，
则m2-2m=8，
所以2016-2m2+4m=2016-2（m2-2m）=2016-2×8=2000．
故答案为2000．
点评 本题考查的是一元二次方程的根即方程的解的定义．一元二次方程的根就是一元二次方程的解，就是能够使方程左右两边相等的未知数的值．即用这个数代替未知数所得式子仍然成立．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
6．
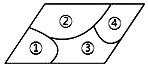小敏不慎将一块平行四边形玻璃打碎成如图的四块，为了能在商店配到一块与原来相同的平行四边形玻璃，他带了两块碎玻璃，其编号应该是（ ）
小敏不慎将一块平行四边形玻璃打碎成如图的四块，为了能在商店配到一块与原来相同的平行四边形玻璃，他带了两块碎玻璃，其编号应该是（ ）| A． | ①，② | B． | ②，③ | C． | ③，④ | D． | ①，④ |
9．已知x+y=$\sqrt{2}$，|x|+|y|=5$\sqrt{2}$，则x-y的值为（ ）
| A． | $±2\sqrt{2}$ | B． | $±3\sqrt{2}$ | C． | $±4\sqrt{2}$ | D． | $±5\sqrt{2}$ |
16．若一元二次方程x2-ax+4=0有两个不相等的实数根，则a的值可以是（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
13．某商场把一个双肩背包按进价提高50%标价，然后再按标价八折出售，这样商场每卖出一个书包仍可赢利8元，则这款双肩包的进价是（ ）
| A． | 16元 | B． | 24元 | C． | 30元 | D． | 40元 |
10．式子$-\sqrt{a{x^3}}$（a＞0）化简的结果是（ ）
| A． | $x\sqrt{-ax}$ | B． | $-x\sqrt{-ax}$ | C． | $x\sqrt{ax}$ | D． | $-x\sqrt{ax}$ |