题目内容
14.没有实数根的一元二次方程是( )| A. | x2=2 | B. | x(x-$\sqrt{3}$)=0 | C. | x2=x-1 | D. | x2-2x+1=0 |
分析 根据根的判别式的值的大小与零的关系来判断根的情况.没有实数根的一元二次方程,即判别式的值是负数的方程.
解答 解:A、△=8>0,方程有两个不相等的实数根,故错误;
B、△=3>0,方程有两个不相等的实数根,故错误;
C、△=-3<0,方程没有实数根,故正确;
D、△=0,方程有两个相等的实数根,故错误.
故选C.
点评 本题考查了一元二次方程根的判别式,总结:一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
相关题目
4.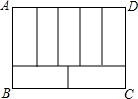 如图,周长为34cm的长方形ABCD被分成7个形状大小完全相同的小长方形,则长方形ABCD的面积为( )
如图,周长为34cm的长方形ABCD被分成7个形状大小完全相同的小长方形,则长方形ABCD的面积为( )
 如图,周长为34cm的长方形ABCD被分成7个形状大小完全相同的小长方形,则长方形ABCD的面积为( )
如图,周长为34cm的长方形ABCD被分成7个形状大小完全相同的小长方形,则长方形ABCD的面积为( )| A. | 49cm2 | B. | 74cm2 | C. | 68cm2 | D. | 70cm2 |
2. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点,则∠ECD=( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点,则∠ECD=( )
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点,则∠ECD=( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点,则∠ECD=( )| A. | 22.5° | B. | 30° | C. | 36° | D. | 45° |
19.用配方法将x2-2x-2=0变形,正确的是( )
| A. | (x-1)2=1 | B. | (x+1)2=3 | C. | (x-1)2=3 | D. | (x+1)2=1 |
4.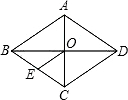 已知,如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=10cm,则OE的长为( )
已知,如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=10cm,则OE的长为( )
 已知,如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=10cm,则OE的长为( )
已知,如图,菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=10cm,则OE的长为( )| A. | 6cm | B. | 5cm | C. | 4cm | D. | 3cm |
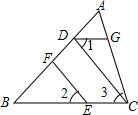 如图,EF⊥AB于F,CD⊥AB于D,点G在AC边上,且∠AGD=∠ACB,
如图,EF⊥AB于F,CD⊥AB于D,点G在AC边上,且∠AGD=∠ACB,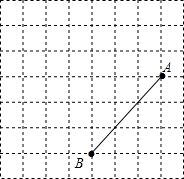 请在网格中建立平面直角坐标系,使得A点的坐标为(4,2).
请在网格中建立平面直角坐标系,使得A点的坐标为(4,2). 如图都是小方格,A,B,C构成三角形,则cosA=$\frac{3}{5}$.
如图都是小方格,A,B,C构成三角形,则cosA=$\frac{3}{5}$.