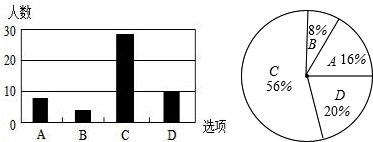
题目内容
5.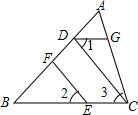 如图,EF⊥AB于F,CD⊥AB于D,点G在AC边上,且∠AGD=∠ACB,
如图,EF⊥AB于F,CD⊥AB于D,点G在AC边上,且∠AGD=∠ACB,(1)求证:EF∥CD;
(2)求证:∠1=∠2.
分析 (1)由垂直的定义可得∠BFE=∠BDC,再根据平行线的判定可证明EF∥CD;
(2)由条件可证明DG∥BC,结合(1)的结论,根据平行线的性质可证明∠1=∠2.
解答 证明:
(1)∵EF⊥AB于F,CD⊥AB于D,
∴∠BFE=∠BDC=90°,
∴EF∥CD;
(2)∵EF∥CD,
∴∠2=∠3,
∵∠AGD=∠ACB,
∴DG∥BC,
∴∠1=∠3
∴∠1=∠2.
点评 本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.

练习册系列答案
相关题目
14.没有实数根的一元二次方程是( )
| A. | x2=2 | B. | x(x-$\sqrt{3}$)=0 | C. | x2=x-1 | D. | x2-2x+1=0 |
15.下列四个多项式中为完全平方式的为( )
| A. | 4a2+2ab+b2 | B. | m2+2mn+n2 | C. | m2n2-mn+1 | D. | 4x2+10x+25 |
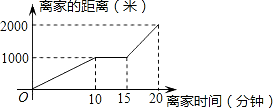 某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.图中描述了他上学的途中离家距离S(米)与离家时间t(分)之间的函数关系.下列说法中正确的个数是( )
某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.图中描述了他上学的途中离家距离S(米)与离家时间t(分)之间的函数关系.下列说法中正确的个数是( )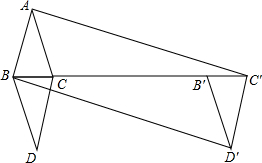 如图,△ABC中,AB=AC=3,BC=2,将△ABC沿BC翻折,得△DBC,再将△DBC沿射线BC方向平移k个距离得三角形D′B′C′,若四边形ABD′C′是矩形,则k=7.
如图,△ABC中,AB=AC=3,BC=2,将△ABC沿BC翻折,得△DBC,再将△DBC沿射线BC方向平移k个距离得三角形D′B′C′,若四边形ABD′C′是矩形,则k=7.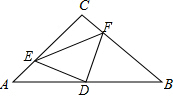 如图,在△ABC中,∠C=90°,CA=CB,D是AB的中点,点E、F在AB、AC边上运动(点E不与A、C重合),且保持AE=CF,连接DE,DF,EF.有下列结论:
如图,在△ABC中,∠C=90°,CA=CB,D是AB的中点,点E、F在AB、AC边上运动(点E不与A、C重合),且保持AE=CF,连接DE,DF,EF.有下列结论: