题目内容
9.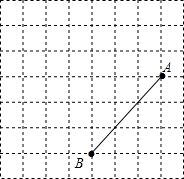 请在网格中建立平面直角坐标系,使得A点的坐标为(4,2).
请在网格中建立平面直角坐标系,使得A点的坐标为(4,2).(1)写出B点的坐标;
(2)将线段AB平移后得到线段A′B,若点A′的坐标为(2,3),画出平移后的线段A′B′,并直接写出点B′的坐标;
(3)已知点P(0,3),请在平面直角坐标系描出点P,并求△PAB的面积S的值.
分析 (1)首先根据A点坐标建立坐标系,进而可得B点坐标;
(2)根据A和A′的坐标可得点A向上平移1个单位,向左平移2个单位,则B点平移方法相同;
(3)利用矩形的面积减去周围多余三角形的面积即可.
解答  解:(1)B(1,-1);
解:(1)B(1,-1);
(2)如图所示:B′(-1,0);
(3)S=4×4-$\frac{1}{2}$×4×1-$\frac{1}{2}$×3×3-$\frac{1}{2}×$1×4=16-4-4.5=7.5.
点评 此题主要考查了作图--平移变换,关键是正确画出坐标系,掌握点的平移规律和坐标的变化.

练习册系列答案
相关题目
4. 实数a在数轴上的位置如图,则下列关系表示正确的是 ( )
实数a在数轴上的位置如图,则下列关系表示正确的是 ( )
 实数a在数轴上的位置如图,则下列关系表示正确的是 ( )
实数a在数轴上的位置如图,则下列关系表示正确的是 ( )| A. | a<1<-a | B. | a<-a<1 | C. | 1<-a<a | D. | -a<a<1 |
14.没有实数根的一元二次方程是( )
| A. | x2=2 | B. | x(x-$\sqrt{3}$)=0 | C. | x2=x-1 | D. | x2-2x+1=0 |

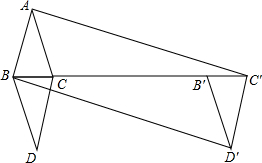 如图,△ABC中,AB=AC=3,BC=2,将△ABC沿BC翻折,得△DBC,再将△DBC沿射线BC方向平移k个距离得三角形D′B′C′,若四边形ABD′C′是矩形,则k=7.
如图,△ABC中,AB=AC=3,BC=2,将△ABC沿BC翻折,得△DBC,再将△DBC沿射线BC方向平移k个距离得三角形D′B′C′,若四边形ABD′C′是矩形,则k=7.
 如图,在△ABC,AC=BC,∠C=90°,CD=1,AD是△ABC的角平分线,DE⊥AB交于点E,则AC的长为$\sqrt{2}$+1.
如图,在△ABC,AC=BC,∠C=90°,CD=1,AD是△ABC的角平分线,DE⊥AB交于点E,则AC的长为$\sqrt{2}$+1.