题目内容
9.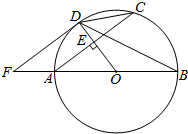 如图,AB是⊙O的直径.半径OD垂直弦AC于点E.F是BA延长线上一点,∠CDB=∠BFD.
如图,AB是⊙O的直径.半径OD垂直弦AC于点E.F是BA延长线上一点,∠CDB=∠BFD.(1)判断DF与⊙O的位置关系,并证明;
(2)若AB=10,AC=8,求DF的长.
分析 (1)利用圆周角定理以及平行线的判定得出∠FDO=90°,进而得出答案;
(2)利用垂径定理得出AE的长,再利用相似三角形的判定与性质得出FD的长.
解答 解:(1)DF与⊙O相切.
∵∠CDB=∠CAB,
又∵∠CDB=∠BFD,
∴∠CAB=∠BFD.
∴AC∥DF.
∵半径OD垂直于弦AC于点E,
∴OD⊥DF.
∴DF与⊙O相切.
(2)∵半径OD垂直于弦AC于点E,AC=8,
∴$AE=\frac{1}{2}AC=\frac{1}{2}×8=4$.
∵AB是⊙O的直径,
∴$OA=OD=\frac{1}{2}AB=\frac{1}{2}×10=5$.
在Rt△AEO中,$OE=\sqrt{O{A^2}-A{E^2}}=\sqrt{{5^2}-{4^2}}=3$.
∵AC∥DF,
∴△OAE∽△OFD.
∴$\frac{OE}{OD}=\frac{AE}{DF}$.
∴$\frac{3}{5}=\frac{4}{DF}$.
∴$DF=\frac{20}{3}$.
点评 此题主要考查了相似三角形的判定与性质以及切线的判定等知识,得出△OAE∽△OFD是解题关键.

练习册系列答案
相关题目
20.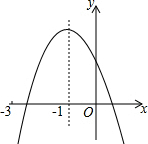 二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴x=-1,下列结论:①2a-b=0;②a+b+c<0;③a-b>am2-bm;④a-$\frac{1}{2}$b+$\frac{1}{4}$c>0;⑤ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=-2.其中正确的有( )
二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴x=-1,下列结论:①2a-b=0;②a+b+c<0;③a-b>am2-bm;④a-$\frac{1}{2}$b+$\frac{1}{4}$c>0;⑤ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=-2.其中正确的有( )
 二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴x=-1,下列结论:①2a-b=0;②a+b+c<0;③a-b>am2-bm;④a-$\frac{1}{2}$b+$\frac{1}{4}$c>0;⑤ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=-2.其中正确的有( )
二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴x=-1,下列结论:①2a-b=0;②a+b+c<0;③a-b>am2-bm;④a-$\frac{1}{2}$b+$\frac{1}{4}$c>0;⑤ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=-2.其中正确的有( )| A. | ①③④ | B. | ①②④⑤ | C. | ②③⑤ | D. | ①③④⑤ |
4.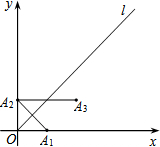 如图,在平面直角坐标系xOy中,函数y=x的图象为直线l,作点A1(1,0)关于直线l的对称点A2,将A2向右平移2个单位得到点A3;再作A3关于直线l的对称点A4,将A4向右平移2个单位得到点A5;….则按此规律,所作出的点A2015的坐标为( )
如图,在平面直角坐标系xOy中,函数y=x的图象为直线l,作点A1(1,0)关于直线l的对称点A2,将A2向右平移2个单位得到点A3;再作A3关于直线l的对称点A4,将A4向右平移2个单位得到点A5;….则按此规律,所作出的点A2015的坐标为( )
 如图,在平面直角坐标系xOy中,函数y=x的图象为直线l,作点A1(1,0)关于直线l的对称点A2,将A2向右平移2个单位得到点A3;再作A3关于直线l的对称点A4,将A4向右平移2个单位得到点A5;….则按此规律,所作出的点A2015的坐标为( )
如图,在平面直角坐标系xOy中,函数y=x的图象为直线l,作点A1(1,0)关于直线l的对称点A2,将A2向右平移2个单位得到点A3;再作A3关于直线l的对称点A4,将A4向右平移2个单位得到点A5;….则按此规律,所作出的点A2015的坐标为( )| A. | (1007,1008) | B. | (1008,1007) | C. | (1006,1007) | D. | (1007,1006) |
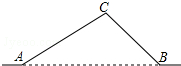 如图,从城市A到B城市的公路需经过城市C,图中AC=100千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两城市间修建一条笔直的公路.
如图,从城市A到B城市的公路需经过城市C,图中AC=100千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两城市间修建一条笔直的公路. 如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.
如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F. 在Rt△ABC中,∠ACB=90°.
在Rt△ABC中,∠ACB=90°.