题目内容
12.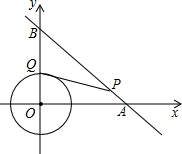 如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P 作⊙O的一条切线PQ,Q为切点,则△OPQ面积的最小值为2$\sqrt{2}$.
如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P 作⊙O的一条切线PQ,Q为切点,则△OPQ面积的最小值为2$\sqrt{2}$.
分析 由P在直线y=-x+6上,设P(m,6-m),连接OQ,OP,由PQ为圆O的切线,得到PQ⊥OQ,在直角三角形OPQ中,利勾股定理列出关系式,配方后利用二次函数的性质即可求出PQ的最小值.
解答 解:∵P在直线y=-x+6上,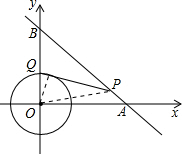
∴设P坐标为(m,6-m),
连接OQ,OP,由PQ为圆O的切线,得到PQ⊥OQ,
在Rt△OPQ中,根据勾股定理得:OP2=PQ2+OQ2,
∴PQ2=m2+(6-m)2-2=2m2-12m+34=2(m-3)2+16,
则当m=3时,切线长PQ的最小值为4.
则△OPQ面积的最小值为$\frac{1}{2}$×4×$\sqrt{2}$=2$\sqrt{2}$
故答案为:2$\sqrt{2}$.
点评 此题考查了一次函数综合题,涉及的知识有:切线的性质,勾股定理,配方法的应用,以及二次函数的性质,熟练掌握二次函数的性质是解本题的关键.

练习册系列答案
相关题目
3. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=35°,则∠B的度数是( )
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=35°,则∠B的度数是( )
 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=35°,则∠B的度数是( )
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=35°,则∠B的度数是( )| A. | 80° | B. | 75° | C. | 70° | D. | 65° |
20.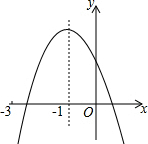 二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴x=-1,下列结论:①2a-b=0;②a+b+c<0;③a-b>am2-bm;④a-$\frac{1}{2}$b+$\frac{1}{4}$c>0;⑤ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=-2.其中正确的有( )
二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴x=-1,下列结论:①2a-b=0;②a+b+c<0;③a-b>am2-bm;④a-$\frac{1}{2}$b+$\frac{1}{4}$c>0;⑤ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=-2.其中正确的有( )
 二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴x=-1,下列结论:①2a-b=0;②a+b+c<0;③a-b>am2-bm;④a-$\frac{1}{2}$b+$\frac{1}{4}$c>0;⑤ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=-2.其中正确的有( )
二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴x=-1,下列结论:①2a-b=0;②a+b+c<0;③a-b>am2-bm;④a-$\frac{1}{2}$b+$\frac{1}{4}$c>0;⑤ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=-2.其中正确的有( )| A. | ①③④ | B. | ①②④⑤ | C. | ②③⑤ | D. | ①③④⑤ |
4.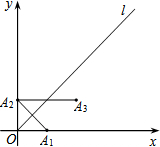 如图,在平面直角坐标系xOy中,函数y=x的图象为直线l,作点A1(1,0)关于直线l的对称点A2,将A2向右平移2个单位得到点A3;再作A3关于直线l的对称点A4,将A4向右平移2个单位得到点A5;….则按此规律,所作出的点A2015的坐标为( )
如图,在平面直角坐标系xOy中,函数y=x的图象为直线l,作点A1(1,0)关于直线l的对称点A2,将A2向右平移2个单位得到点A3;再作A3关于直线l的对称点A4,将A4向右平移2个单位得到点A5;….则按此规律,所作出的点A2015的坐标为( )
 如图,在平面直角坐标系xOy中,函数y=x的图象为直线l,作点A1(1,0)关于直线l的对称点A2,将A2向右平移2个单位得到点A3;再作A3关于直线l的对称点A4,将A4向右平移2个单位得到点A5;….则按此规律,所作出的点A2015的坐标为( )
如图,在平面直角坐标系xOy中,函数y=x的图象为直线l,作点A1(1,0)关于直线l的对称点A2,将A2向右平移2个单位得到点A3;再作A3关于直线l的对称点A4,将A4向右平移2个单位得到点A5;….则按此规律,所作出的点A2015的坐标为( )| A. | (1007,1008) | B. | (1008,1007) | C. | (1006,1007) | D. | (1007,1006) |
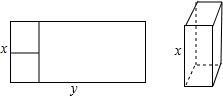 如图,在矩形中截取两个相同的正方形作为立方体的上下底面,剩余的矩形作为立方体的侧面,刚好能组成立方体.设矩形的长和宽分别为y和x,则y与x的函数图象大致是( )
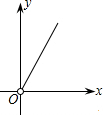
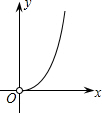
如图,在矩形中截取两个相同的正方形作为立方体的上下底面,剩余的矩形作为立方体的侧面,刚好能组成立方体.设矩形的长和宽分别为y和x,则y与x的函数图象大致是( )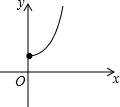
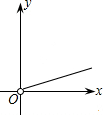
 如图,一圆与平面直角坐标系中的x轴切于点A(4,0),与y轴交于点B(0,2),C(0,8),则该圆的直径为10.
如图,一圆与平面直角坐标系中的x轴切于点A(4,0),与y轴交于点B(0,2),C(0,8),则该圆的直径为10.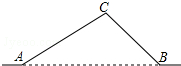 如图,从城市A到B城市的公路需经过城市C,图中AC=100千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两城市间修建一条笔直的公路.
如图,从城市A到B城市的公路需经过城市C,图中AC=100千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两城市间修建一条笔直的公路.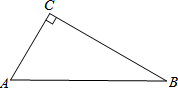 在Rt△ABC中,∠ACB=90°.
在Rt△ABC中,∠ACB=90°.