题目内容
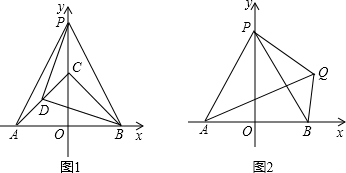
 如图,△ABC中,∠ACB=90°,AD平分∠ACB交BC于D,DE⊥AB于E,且AE=BE,若DE=0.5,AD=1.5cm,则BC=
如图,△ABC中,∠ACB=90°,AD平分∠ACB交BC于D,DE⊥AB于E,且AE=BE,若DE=0.5,AD=1.5cm,则BC=考点:角平分线的性质,勾股定理
专题:
分析:根据角平分线上的点到角的两边距离相等可得CD=DE,再根据线段垂直平分线上的点到两端点的距离相等可得BD=AD,然后根据BC=BD+CD代入数据计算即可得解.
解答:解:∵AD平分∠ACB交BC于D,DE⊥AB,∠ACB=90°,
∴CD=DE=0.5cm,
∵DE⊥AB,AE=BE,
∴BD=AD=1.5,
∴BC=BD+CD=1.5+0.5=2cm.
故答案为:2.
∴CD=DE=0.5cm,
∵DE⊥AB,AE=BE,
∴BD=AD=1.5,
∴BC=BD+CD=1.5+0.5=2cm.
故答案为:2.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,线段垂直平分线上的点到两端点的距离相等的性质,熟记性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在△ABC中,DE是中位线,若∠ADE=60°,BC=8cm,则∠B=
如图,在△ABC中,DE是中位线,若∠ADE=60°,BC=8cm,则∠B=