题目内容
7.为促进朗诵艺术的普及、发展,挖掘播音主持人才,某校初二年级举办朗诵大赛,凡凡同学根据比赛中九位评委所给的某位参赛选手的分数,制作了一个表格,如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )| 中位数 | 众数 | 平均数 | 方差 |
| 9.2 | 9.3 | 9.1 | 0.3 |
| A. | 中位数 | B. | 众数 | C. | 平均数 | D. | 方差 |
分析 根据中位数的定义:位于中间位置或中间两数的平均数可以得到去掉一个最高分和一个最低分不影响中位数.
解答 解:去掉一个最高分和一个最低分对中位数没有影响,
故选:A.
点评 本题考查了统计量的选择,解题的关键是了解中位数的定义,难度不大.

练习册系列答案
相关题目
17.进入夏季后某款空调供不应求,厂家加班生产并销售,在第一个产销期的12天中,为提高产量,从第5天开始增加了工时生产成本,每台空调的成本P(元)与时间x(天)的关系如表:
已知每天生产的空调数量y(台)与时间x(天)近似满足函数关系y=2x+16,每台空调的出售价格为1400元.
请解答下列问题:
(1)设厂家的日销售利润为W元,求W(元)与时间x(天)的函数关系式;
(2)确定该厂哪一天获得最大利润,最大利润是多少?
(3)设厂家在第一个产销期,获得最大利润时的成本为P1,日生产量为y1.
现计划从第13天开始,按每台成本P1元,每台生产y1台进行生产并完全售出,但由于机器损耗等原因,实际平均每台空调的成本比统计增加了a%,使得厂家10天的销售利润与原计划的8天的销售利润持平,求a的值.
| 时间x(天) | 每台空调的成本P(元) |
| 0<x≤5 | P=400 |
| 5<x≤12 | P=40x+200 |
请解答下列问题:
(1)设厂家的日销售利润为W元,求W(元)与时间x(天)的函数关系式;
(2)确定该厂哪一天获得最大利润,最大利润是多少?
(3)设厂家在第一个产销期,获得最大利润时的成本为P1,日生产量为y1.
现计划从第13天开始,按每台成本P1元,每台生产y1台进行生产并完全售出,但由于机器损耗等原因,实际平均每台空调的成本比统计增加了a%,使得厂家10天的销售利润与原计划的8天的销售利润持平,求a的值.
2.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
12. 如图,数轴上的四个点A、B、C、D位置如图所示,它们分别对应四个实数a、b、c、d,若a+c=0,AB<BC,则下列各式正确的是( )
如图,数轴上的四个点A、B、C、D位置如图所示,它们分别对应四个实数a、b、c、d,若a+c=0,AB<BC,则下列各式正确的是( )
 如图,数轴上的四个点A、B、C、D位置如图所示,它们分别对应四个实数a、b、c、d,若a+c=0,AB<BC,则下列各式正确的是( )
如图,数轴上的四个点A、B、C、D位置如图所示,它们分别对应四个实数a、b、c、d,若a+c=0,AB<BC,则下列各式正确的是( )| A. | bc>0 | B. | b-d>0 | C. | b+c>0 | D. | |a|>|d| |
19.数轴上的两个数-3与a,并且a>-3,它们之间的距离可以表示为( )
| A. | 3-a | B. | -3-a | C. | a-3 | D. | a+3 |
16.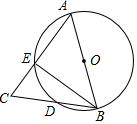 如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,则∠EBC等于( )
如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,则∠EBC等于( )
 如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,则∠EBC等于( )
如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,则∠EBC等于( )| A. | 22.5° | B. | 23° | C. | 25° | D. | 30° |
17. 如图是底面为正方形的长方体,下面有关它的三个视图的说法正确的是( )
如图是底面为正方形的长方体,下面有关它的三个视图的说法正确的是( )
 如图是底面为正方形的长方体,下面有关它的三个视图的说法正确的是( )
如图是底面为正方形的长方体,下面有关它的三个视图的说法正确的是( )| A. | 俯视图与主视图相同 | B. | 左视图与主视图相同 | ||
| C. | 左视图与俯视图相同 | D. | 三个视图都相同 |
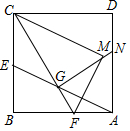 在正方形ABCD中,AB=2$\sqrt{5}$+2,E是边BC的中点,F是AB上一点,线段AE、CF交于点G,且CE=EG,将△CBF沿CF翻折,使得点B落在点M,连接GM并延长交AD于点N,则△AGN的面积为$\frac{16}{5}$$\sqrt{5}$.
在正方形ABCD中,AB=2$\sqrt{5}$+2,E是边BC的中点,F是AB上一点,线段AE、CF交于点G,且CE=EG,将△CBF沿CF翻折,使得点B落在点M,连接GM并延长交AD于点N,则△AGN的面积为$\frac{16}{5}$$\sqrt{5}$.