题目内容
17.进入夏季后某款空调供不应求,厂家加班生产并销售,在第一个产销期的12天中,为提高产量,从第5天开始增加了工时生产成本,每台空调的成本P(元)与时间x(天)的关系如表:| 时间x(天) | 每台空调的成本P(元) |
| 0<x≤5 | P=400 |
| 5<x≤12 | P=40x+200 |
请解答下列问题:
(1)设厂家的日销售利润为W元,求W(元)与时间x(天)的函数关系式;
(2)确定该厂哪一天获得最大利润,最大利润是多少?
(3)设厂家在第一个产销期,获得最大利润时的成本为P1,日生产量为y1.
现计划从第13天开始,按每台成本P1元,每台生产y1台进行生产并完全售出,但由于机器损耗等原因,实际平均每台空调的成本比统计增加了a%,使得厂家10天的销售利润与原计划的8天的销售利润持平,求a的值.
分析 (1)分0<x≤5、5<x≤12,根据“总利润=单件利润×销售量”列出函数解析式;
(2)结合x的范围,分别根据一次函数和二次函数的增减性求解可得;
(3)先根据题意求得y1、P1,再由“厂家10天的销售利润与原计划的8天的销售利润持平”列方程求解可得.
解答 解:(1)当0<x≤5时,W=y(1400-P)=(2x+16)(1400-400)=2000x+16000;
当5<x≤12时,W=y(1400-P)=(2x+16)[1400-(40x+20)]=-80x2+1760x+19200.
(2)当0<x≤5时,W=2000x+16000,
∵2000>0,W随x的增大而增大,
∴当x=5时,W有最大值为26000元;
当5<x≤12时,W=-80x2+1760x+19200=-80(x-11)2+28880,
∴当x=11时,W有最大值28880元,
综上,第11天的利润最大,最大利润是28880元;
(3)y1=2×11+16=38件,P1=40×11+200=640元,
由题意得:[1400-640(1+a%)]×38×10=28880×8,
解得:a=23.75,
∴a的值为23.75.
点评 本题主要考查二次函数的应用及一元一次方程的应用,理解题意找到题目蕴含的相等关系是解题的关键.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
8.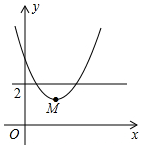 如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y=$\frac{1}{2}{x^2}$+bx+c的顶点,则抛物线y=$\frac{1}{2}{x^2}$+bx+c与直线y=1交点的个数是( )
如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y=$\frac{1}{2}{x^2}$+bx+c的顶点,则抛物线y=$\frac{1}{2}{x^2}$+bx+c与直线y=1交点的个数是( )
 如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y=$\frac{1}{2}{x^2}$+bx+c的顶点,则抛物线y=$\frac{1}{2}{x^2}$+bx+c与直线y=1交点的个数是( )
如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y=$\frac{1}{2}{x^2}$+bx+c的顶点,则抛物线y=$\frac{1}{2}{x^2}$+bx+c与直线y=1交点的个数是( )| A. | 0个或1个 | B. | 0个或2个 | C. | 1个或2个 | D. | 0个、1个或2个 |
7.为促进朗诵艺术的普及、发展,挖掘播音主持人才,某校初二年级举办朗诵大赛,凡凡同学根据比赛中九位评委所给的某位参赛选手的分数,制作了一个表格,如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
| 中位数 | 众数 | 平均数 | 方差 |
| 9.2 | 9.3 | 9.1 | 0.3 |
| A. | 中位数 | B. | 众数 | C. | 平均数 | D. | 方差 |
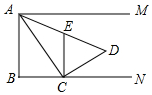 如图,射线AM平行于射线BN,∠B=90°,AB=4,C是射线BN上的一个动点,连接AC,作CD⊥AC,且AC=2CD,过C作CE⊥BN交AD于点E,设BC长为a.
如图,射线AM平行于射线BN,∠B=90°,AB=4,C是射线BN上的一个动点,连接AC,作CD⊥AC,且AC=2CD,过C作CE⊥BN交AD于点E,设BC长为a.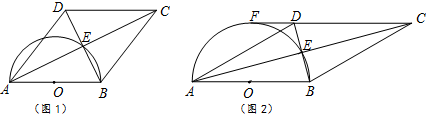
 如图,矩形ABCD中,AB=10,BC=8,P为AD的中点,将△ABP沿BP翻折至△EBP(点A落到点E处),连接DE,则图中与∠APB相等的角的个数为( )
如图,矩形ABCD中,AB=10,BC=8,P为AD的中点,将△ABP沿BP翻折至△EBP(点A落到点E处),连接DE,则图中与∠APB相等的角的个数为( )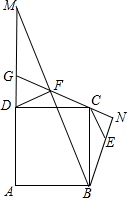 如图,等腰Rt△BNF的直角边FN所在的直线过正方形ABCD的顶点C,且与AD的延长线交于G,BF、AD的延长线交于M,连接DF,CE∥BM交BN于E.
如图,等腰Rt△BNF的直角边FN所在的直线过正方形ABCD的顶点C,且与AD的延长线交于G,BF、AD的延长线交于M,连接DF,CE∥BM交BN于E.