题目内容
15.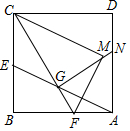 在正方形ABCD中,AB=2$\sqrt{5}$+2,E是边BC的中点,F是AB上一点,线段AE、CF交于点G,且CE=EG,将△CBF沿CF翻折,使得点B落在点M,连接GM并延长交AD于点N,则△AGN的面积为$\frac{16}{5}$$\sqrt{5}$.
在正方形ABCD中,AB=2$\sqrt{5}$+2,E是边BC的中点,F是AB上一点,线段AE、CF交于点G,且CE=EG,将△CBF沿CF翻折,使得点B落在点M,连接GM并延长交AD于点N,则△AGN的面积为$\frac{16}{5}$$\sqrt{5}$.
分析 先作GH⊥BC于H,交AN于J,则GH∥AB,即可得到HG:HE=AB:BE=2:1,设HE=m,则HG=2m,EG=$\sqrt{5}$m,进而得到BC=2GE=2$\sqrt{5}$m,GJ=2$\sqrt{5}$m-2m,根据AB=2$\sqrt{5}$+2=BC,可得m=1+$\frac{\sqrt{5}}{5}$,再根据$\frac{GH}{GJ}$=$\frac{BE}{NA}$,可得AN=(5-$\sqrt{5}$)m,最后根据△AGN的面积=$\frac{1}{2}$AN×GJ,进行计算即可.
解答  解:如图所示,作GH⊥BC于H,交AN于J,连接BG,则GH∥AB,
解:如图所示,作GH⊥BC于H,交AN于J,连接BG,则GH∥AB,
∴HG:HE=AB:BE=2:1,
设HE=m,则HG=2m,EG=$\sqrt{5}$m,
∵E是边BC的中点,CE=EG,
∴BC=2GE=2$\sqrt{5}$m,GJ=2$\sqrt{5}$m-2m,
∵AB=2$\sqrt{5}$+2=BC,
∴2$\sqrt{5}$+2=2$\sqrt{5}$m,
解得m=1+$\frac{\sqrt{5}}{5}$,
∵EG=CE=BE,
∴∠BGC=$\frac{1}{2}$×180°=90°,即BG⊥CF,
又∵BM⊥CF,
∴B,G,M在同一直线上,
又∵BE∥AN,
∴△GBE∽△GNA,
∴$\frac{GH}{GJ}$=$\frac{BE}{NA}$,即$\frac{2m}{2\sqrt{5}m-2m}$=$\frac{\sqrt{5}m}{AN}$,
解得AN=(5-$\sqrt{5}$)m,
∴△AGN的面积=$\frac{1}{2}$AN×GJ
=$\frac{1}{2}$(5-$\sqrt{5}$)m×(2$\sqrt{5}$m-2m)
=$\sqrt{5}$($\sqrt{5}$-1)2m2
=$\sqrt{5}$($\sqrt{5}$-1)2(1+$\frac{\sqrt{5}}{5}$)2
=$\frac{16}{5}$$\sqrt{5}$,
故答案为:$\frac{16}{5}$$\sqrt{5}$.
点评 本题主要考查了折叠问题,正方形的性质以及相似三角形的判定与性质的综合应用,解决问题的关键是依据相似三角形的对应边成比例列式计算,求出△ANG的底边与高.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| A. |  | B. |  | C. |  | D. |  |
| 中位数 | 众数 | 平均数 | 方差 |
| 9.2 | 9.3 | 9.1 | 0.3 |
| A. | 中位数 | B. | 众数 | C. | 平均数 | D. | 方差 |