题目内容
18．不等式组$\left\{\begin{array}{l}{\frac{1}{2}x≤1}\\{2-x＜3}\end{array}\right.$的最小整数解为（ ）| A． | -1 | B． | 0 | C． | 1 | D． | 2 |
分析 先求出不等式组中每个不等式的解集，然后求出其公共解集，最后求其最小整数解即可．
解答 解：$\left\{\begin{array}{l}{\frac{1}{2}x≤1①}\\{2-x＜3②}\end{array}\right.$
由①得x≤2；
由②得x＞-1；
不等式组的解集为-1＜x≤2；
所以其最小整数解为0．
故选B．
点评 本题旨在考查不等式组的解法及整数解的确定．求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．
练习册系列答案
相关题目
8．
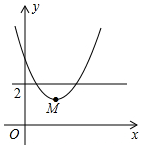如图，平面直角坐标系中，点M是直线y=2与x轴之间的一个动点，且点M是抛物线y=$\frac{1}{2}{x^2}$+bx+c的顶点，则抛物线y=$\frac{1}{2}{x^2}$+bx+c与直线y=1交点的个数是（ ）
如图，平面直角坐标系中，点M是直线y=2与x轴之间的一个动点，且点M是抛物线y=$\frac{1}{2}{x^2}$+bx+c的顶点，则抛物线y=$\frac{1}{2}{x^2}$+bx+c与直线y=1交点的个数是（ ）| A． | 0个或1个 | B． | 0个或2个 | C． | 1个或2个 | D． | 0个、1个或2个 |
13．
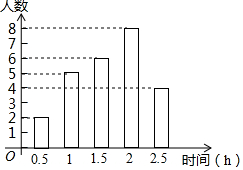某班25名同学在一周内做家务劳动时间如图所示，则做家务劳动时间的众数和中位数分别是（ ）
某班25名同学在一周内做家务劳动时间如图所示，则做家务劳动时间的众数和中位数分别是（ ）| A． | 2和1.5 | B． | 1.5和1.5 | C． | 2和2.5 | D． | 1.75和2 |
7．为促进朗诵艺术的普及、发展，挖掘播音主持人才，某校初二年级举办朗诵大赛，凡凡同学根据比赛中九位评委所给的某位参赛选手的分数，制作了一个表格，如果去掉一个最高分和一个最低分，则表中数据一定不发生变化的是（ ）
| 中位数 | 众数 | 平均数 | 方差 |
| 9.2 | 9.3 | 9.1 | 0.3 |
| A． | 中位数 | B． | 众数 | C． | 平均数 | D． | 方差 |
