题目内容
16.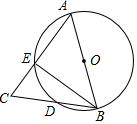 如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,则∠EBC等于( )
如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,则∠EBC等于( )| A. | 22.5° | B. | 23° | C. | 25° | D. | 30° |
分析 首先由圆周角定理、三角形内角和定理求得∠ABE=45°;其次由等腰△ABC的性质.三角形内角和定理求得∠ABC=67.5°;最后,由图形知∠EBC=∠ABC-∠ABE,据此求解.
解答 解:∵AB为⊙O的直径,点E在⊙O上,
∴∠AEB=90°.
∵∠BAC=45°,
∴∠ABE=45°.
又∵在△ABC中,AB=AC,
∴∠ABC=∠C,∠ABC+∠C=180°-45°=135°,
∴∠ABC=67.5°,
∴∠EBC=∠ABC-∠ABE=67.5°-45°=22.5°.
故选A.
点评 本题考查了圆周角定理、等腰三角形的性质.注意:在利用圆周角定理时,必须说明点E在⊙O上.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
7.为促进朗诵艺术的普及、发展,挖掘播音主持人才,某校初二年级举办朗诵大赛,凡凡同学根据比赛中九位评委所给的某位参赛选手的分数,制作了一个表格,如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
| 中位数 | 众数 | 平均数 | 方差 |
| 9.2 | 9.3 | 9.1 | 0.3 |
| A. | 中位数 | B. | 众数 | C. | 平均数 | D. | 方差 |
1. 如图,点A、B、C在⊙O上,∠OAB=25°,则∠ACB的度数是( )
如图,点A、B、C在⊙O上,∠OAB=25°,则∠ACB的度数是( )
 如图,点A、B、C在⊙O上,∠OAB=25°,则∠ACB的度数是( )
如图,点A、B、C在⊙O上,∠OAB=25°,则∠ACB的度数是( )| A. | 50° | B. | 65° | C. | 115° | D. | 135° |
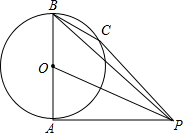 如图,AB为⊙O的直径,过⊙O外一点P作圆的两条切线,切点分别为点A和点C,连接BC和OP.
如图,AB为⊙O的直径,过⊙O外一点P作圆的两条切线,切点分别为点A和点C,连接BC和OP.