题目内容
11. 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,是它们离甲地距离y(千米)与时间x(小时)之间的函数关系图象,请根据图象解答下列问题:
甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,是它们离甲地距离y(千米)与时间x(小时)之间的函数关系图象,请根据图象解答下列问题:(1)线段CD表示轿车在途中停留了0.5小时;
(2)直线OA和直线DE的交点坐标可以看做方程组$\left\{\begin{array}{l}{60x-y=0}\\{110x-y=195}\end{array}\right.$的解.
分析 (1)利用图象得出CD这段时间为2.5-2=0.5,得出答案即可;
(2)利用D点坐标为:(2.5,80),E点坐标为:(4.5,300),求出函数解析式,再根据一次函数与方程组的关系解答即可.
解答 解:(1)利用图象可得:线段CD表示轿车在途中停留了:2.5-2=0.5小时;
(2)根据D点坐标为:(2.5,80),E点坐标为:(4.5,300),
代入y=kx+b,得:
$\left\{\begin{array}{l}{80=2.5k+b}\\{300=4.5k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=110}\\{b=-195}\end{array}\right.$,
故线段DE对应的函数解析式为:y=110x-195(2.5≤x≤4.5);
∵A点坐标为:(5,300),
代入解析式y=ax得,
300=5a,
解得:a=60,
故y=60x,
所以直线OA和直线DE的交点坐标可以看做方程组$\left\{\begin{array}{l}{60x-y=0}\\{110x-y=195}\end{array}\right.$的解.
故答案为:0.5;$\left\{\begin{array}{l}{60x-y=0}\\{110x-y=195}\end{array}\right.$.
点评 此题主要考查了一次函数的应用和待定系数法求一次函数解析式,根据已知得出函数解析式利用图象分析得出是解题关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
2.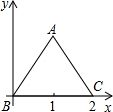 如图,边长为2的等边△ABC以点B为旋转中心,逆时针旋转60°时,点A的对应点的坐标( )
如图,边长为2的等边△ABC以点B为旋转中心,逆时针旋转60°时,点A的对应点的坐标( )
 如图,边长为2的等边△ABC以点B为旋转中心,逆时针旋转60°时,点A的对应点的坐标( )
如图,边长为2的等边△ABC以点B为旋转中心,逆时针旋转60°时,点A的对应点的坐标( )| A. | (1,$\sqrt{3}$) | B. | (1,-$\sqrt{3}$) | C. | (-1,$\sqrt{3}$) | D. | (-1,-$\sqrt{3}$) |
6.某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.设分配给甲店A型产品x件.两商店销售这两种产品每件的利润(元)如下表:
(1)分配给乙店B型产品x-10件(用含x的代数式表示).
(2)设这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并直接写出x的取值范围.
(3)若公司要求总利润不低于17560元,有几种不同分配方案?哪种方案总利润最大?请求出最大利润.
| A型利润 | B型利润 | |
| 甲店 | 200 | 170 |
| 乙店 | 160 | 150 |
(2)设这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并直接写出x的取值范围.
(3)若公司要求总利润不低于17560元,有几种不同分配方案?哪种方案总利润最大?请求出最大利润.
16.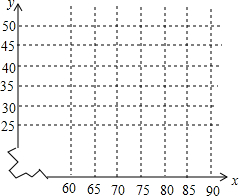 某公司研发出一种新产品,每件成本50元,该公司决定在某地进行试销售,结果发现每件产品的销售单价x(元)与产品的日销售量y(件)之间存在一定的关系,如下表所示:
某公司研发出一种新产品,每件成本50元,该公司决定在某地进行试销售,结果发现每件产品的销售单价x(元)与产品的日销售量y(件)之间存在一定的关系,如下表所示:
(1)把上表中x,y的各组对应值作为点的坐标,在平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;.
(2)求销售价定为80元时,每日的销售利润.
 某公司研发出一种新产品,每件成本50元,该公司决定在某地进行试销售,结果发现每件产品的销售单价x(元)与产品的日销售量y(件)之间存在一定的关系,如下表所示:
某公司研发出一种新产品,每件成本50元,该公司决定在某地进行试销售,结果发现每件产品的销售单价x(元)与产品的日销售量y(件)之间存在一定的关系,如下表所示:| x(元) | 60 | 65 | 70 | 75 | … |
| y (件) | 40 | 35 | 30 | 25 | … |
(2)求销售价定为80元时,每日的销售利润.
 如图,△ABC中,∠ACB=90°,沿CD边折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=22°,则∠BDC等于67°.
如图,△ABC中,∠ACB=90°,沿CD边折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=22°,则∠BDC等于67°. 如图,AB是半圆的直径,点O为圆心,点P沿OA→$\widehat{AB}$→BO匀速运动一周,设OP的长为s,运动时间为t,则s与t的函数关系图象大致是( )
如图,AB是半圆的直径,点O为圆心,点P沿OA→$\widehat{AB}$→BO匀速运动一周,设OP的长为s,运动时间为t,则s与t的函数关系图象大致是( )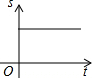


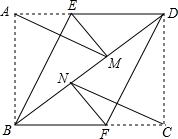 在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,折痕DF交BC于点F.
在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,折痕DF交BC于点F.