题目内容
4.先化简,再求值:$\frac{{a}^{2}-{b}^{2}}{ab}$÷($\frac{1}{a}$+$\frac{1}{b}$).其中a=-2,b=1.分析 原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,把a与b的值代入计算即可求出值.
解答 解:原式=$\frac{{a}^{2}-{b}^{2}}{ab}$÷$\frac{a+b}{ab}$=$\frac{(a-b)(a+b)}{ab}$•$\frac{ab}{a+b}$=a-b,
当a=-2,b=1时,原式=-2-1=-3.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.在同一直角坐标系中,若正比例函数y=k1x的图象与反比例函数$y=\frac{k_2}{x}$的图象没有公共点,则( )
| A. | k1k2<0 | B. | k1k2>0 | C. | k1+k2<0 | D. | k1+k2>0 |
12.无理数a满足:2<a<3,那么a可能是( )
| A. | $\sqrt{10}$ | B. | $\sqrt{6}$ | C. | 2.5 | D. | $\frac{20}{7}$ |
16.在0,-2,-1,3这四个数中,最小的数是( )
| A. | 3 | B. | -1 | C. | 0 | D. | -2 |
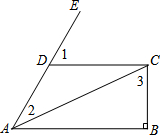 如图,CD∥AB,CB⊥AB,∠1=60°,∠2=40°,则∠3=70°.
如图,CD∥AB,CB⊥AB,∠1=60°,∠2=40°,则∠3=70°.
 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,是它们离甲地距离y(千米)与时间x(小时)之间的函数关系图象,请根据图象解答下列问题:
甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,是它们离甲地距离y(千米)与时间x(小时)之间的函数关系图象,请根据图象解答下列问题: