题目内容
1.先化简,再选一个喜欢的值代入并求值:$\frac{x}{x-2}$÷$\frac{{x}^{2}-2x}{{x}^{2}-4}$-$\frac{2}{x-2}$.分析 原式利用除法法则变形,约分得到最简结果,把x=1代入计算即可求出值.
解答 解:$\frac{x}{x-2}$÷$\frac{{x}^{2}-2x}{{x}^{2}-4}$-$\frac{2}{x-2}$,
=$\frac{x}{x-2}$×$\frac{(x+2)(x-2)}{x(x-2)}$-$\frac{2}{x-2}$,
=$\frac{x+2-2}{x-2}$
=$\frac{x}{x-2}$,
当x=1时,原式=$\frac{1}{1-2}$=-1.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
11.已知直线y1=2x与直线y2=-2x+4相交于点A.有以下结论:①点A的坐标为A(1,2);②当x=1时,两个函数值相等;③当x<1时,y1<y2;④直线y1=2x与直线y2=2x-4在平面直角坐标系中的位置关系是平行.其中正确的是( )
| A. | .①③④ | B. | .②③ | C. | .①②③④ | D. | .①②③ |
12.一元二次方程式x2-8x=48可表示成(x-a)2=48+b的形式,其中a、b为整数,求a+b之值为何( )
| A. | 20 | B. | 12 | C. | -12 | D. | -20 |
9.若3am+2b与ab2n-1是同类项,则m+n的值是( )
| A. | -1 | B. | -5 | C. | 2 | D. | 0 |
16.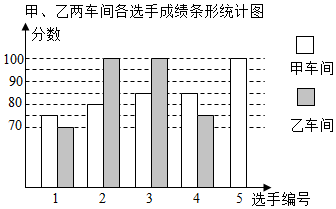 某厂举办职工技能大赛,甲、乙两个车间各派5名选手参加,他们的分数见图表:
某厂举办职工技能大赛,甲、乙两个车间各派5名选手参加,他们的分数见图表:
根据图标信息,解答问题:
(1)x=100,补全条形统计图;
(2)甲车间5名选手的平均分为85,乙车间5名选手的平均分为85;
(3)分别求甲、乙两车间5名选手成绩的方差;判断哪个车间选手的成绩较为稳定.
 某厂举办职工技能大赛,甲、乙两个车间各派5名选手参加,他们的分数见图表:
某厂举办职工技能大赛,甲、乙两个车间各派5名选手参加,他们的分数见图表:| 1号 | 2号 | 3号 | 4号 | 5号 | |
| 甲车间 | 75 | 80 | 85 | 85 | 100 |
| 乙车间 | 70 | 100 | x | 75 | 80 |
(1)x=100,补全条形统计图;
(2)甲车间5名选手的平均分为85,乙车间5名选手的平均分为85;
(3)分别求甲、乙两车间5名选手成绩的方差;判断哪个车间选手的成绩较为稳定.
13.外心在三角形的一边上的三角形形状一定为( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 等腰三角形 |
11.用代数式表示“a的5倍与b的和的平方”,正确的是( )
| A. | (5a+b)2 | B. | 5(a+b)2 | C. | 5a+b2 | D. | (a+5b)2 |
 如图,四边形ABCD的对角线相交于O点,AD=BC,作AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,且DE=BF,则下列结论:
如图,四边形ABCD的对角线相交于O点,AD=BC,作AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,且DE=BF,则下列结论: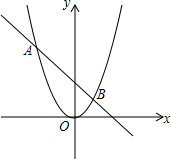 如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-4,8),B(2,2),则关于x的方程ax2-bx-c=0的解为x1=-4,x2=2.
如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-4,8),B(2,2),则关于x的方程ax2-bx-c=0的解为x1=-4,x2=2.