题目内容
10.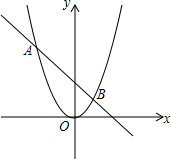 如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-4,8),B(2,2),则关于x的方程ax2-bx-c=0的解为x1=-4,x2=2.
如图,抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-4,8),B(2,2),则关于x的方程ax2-bx-c=0的解为x1=-4,x2=2.
分析 方程ax2-bx-c=0,即ax2=bx+c的解即为抛物线y=ax2与直线y=bx+c交点的横坐标,由函数图象可得答案.
解答 解:方程ax2-bx-c=0,即ax2=bx+c的解即为方程组$\left\{\begin{array}{l}{y=a{x}^{2}}\\{y=bx+c}\end{array}\right.$中x的值,
由y=ax2与y=bx+c的两个交点坐标分别为A(-4,8),B(2,2)知,
方程组$\left\{\begin{array}{l}{y=a{x}^{2}}\\{y=bx+c}\end{array}\right.$的解为$\left\{\begin{array}{l}{{x}_{1}=-4}\\{{y}_{1}=8}\end{array}\right.$、$\left\{\begin{array}{l}{{x}_{2}=2}\\{{y}_{2}=2}\end{array}\right.$,
∴关于x的方程ax2-bx-c=0的解为x1=-4,x2=2,
故答案为:x1=-4,x2=2.
点评 本题考查抛物线与x轴交点、一次函数的应用、一元二次方程等知识,解题的关键是灵活运用所学知识,学会利用图象法解决实际问题.

练习册系列答案
相关题目
20.下列图形既是中心对称图形又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
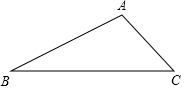 如图,在△ABC中,∠BAC是钝角,按要求画图(不写作法,保留作图痕迹,指出所求)
如图,在△ABC中,∠BAC是钝角,按要求画图(不写作法,保留作图痕迹,指出所求)
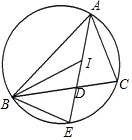 如图,点I是△ABC的内心,AI的延长线与边BC相交于点D,与△ABC的外接圆相交于点C.
如图,点I是△ABC的内心,AI的延长线与边BC相交于点D,与△ABC的外接圆相交于点C.