题目内容
12．一元二次方程式x2-8x=48可表示成（x-a）2=48+b的形式，其中a、b为整数，求a+b之值为何（ ）| A． | 20 | B． | 12 | C． | -12 | D． | -20 |
分析 将一元二次方程式x2-8x=48配方，可求a、b，再代入代数式即可求解．
解答 解：x2-8x=48，
x2-8x+16=48+16，
（x-4）2=48+16，
a=4，b=16，
a+b=20．
故选：A．
点评 此题考查了配方法解一元二次方程，解题时要注意解题步骤的准确应用．选择用配方法解一元二次方程时，最好使方程的二次项的系数为1，一次项的系数是2的倍数．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
2．
一个空心的圆柱如图，那么它的左视图是（ ）
一个空心的圆柱如图，那么它的左视图是（ ）| A． |  | B． |  | C． |  | D． |  |
20．下列图形既是中心对称图形又是轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
7．
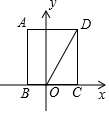如图，矩形ABCD的边BC在x轴上，点A在第二象限，点D在第一象限，AB=2$\sqrt{3}$，OD=4，将矩形ABCD绕点O旋转，使点D落在x轴上，则点C对应点的坐标是（ ）
如图，矩形ABCD的边BC在x轴上，点A在第二象限，点D在第一象限，AB=2$\sqrt{3}$，OD=4，将矩形ABCD绕点O旋转，使点D落在x轴上，则点C对应点的坐标是（ ）| A． | （-$\sqrt{3}$，1） | B． | （-1，$\sqrt{3}$） | C． | （-1，$\sqrt{3}$）或（1，-$\sqrt{3}$） | D． | （-$\sqrt{3}$，1）或（1，-$\sqrt{3}$） |
17．下列命题中是真命题的是（ ）
| A． | 线段垂直平分线上的点到这条线段的两个端点的距离相等 | |
| B． | 有两边及一角相等的两个三角形全等 | |
| C． | 一个图形和经过它旋转所得的图形中，对应的所连的线段平行且相等 | |
| D． | 对角线相等的四边形是平行四边形 |
