题目内容
6. 如图,四边形ABCD的对角线相交于O点,AD=BC,作AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,且DE=BF,则下列结论:
如图,四边形ABCD的对角线相交于O点,AD=BC,作AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,且DE=BF,则下列结论:①AE=CF;
②AO=CO;
③AC=EF;
④AC⊥EF;
⑤四边形AECF是菱形;
⑥四边形ABCD为平行四边形;
其中正确结论的个数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据平行四边形的性质与判定以及全等三角形的判定与性质分别分析得出即可.
解答 解:∵AE⊥BD于点E,CF⊥BD于点F,∴∠AED=∠CFB=90°,
在Rt△ADE和Rt△CBF中,$\left\{\begin{array}{l}{AD=BC}\\{DE=BF}\end{array}\right.$,
∴Rt△ADE≌Rt△CBF(HL),
∴AE=CF,①正确;
∵AE⊥BD于点E,CF⊥BD于点F,
∴AE∥FC,
∵AE=CF,
∴四边形CFAE是平行四边形,
∴AO=CO,②正确,
没有条件证出四边形CFAE是矩形或菱形,
∴③错误,④错误,⑤错误;
∵Rt△ADE≌Rt△CBF,
∴∠ADE=∠CBF,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形,⑥正确;
故选:B.
点评 此题主要考查了平行四边形的性质与判定以及全等三角形的判定与性质等知识,得出Rt△ADE≌Rt△CBF是解题关键.

练习册系列答案
相关题目
17.下列命题中是真命题的是( )
| A. | 线段垂直平分线上的点到这条线段的两个端点的距离相等 | |
| B. | 有两边及一角相等的两个三角形全等 | |
| C. | 一个图形和经过它旋转所得的图形中,对应的所连的线段平行且相等 | |
| D. | 对角线相等的四边形是平行四边形 |
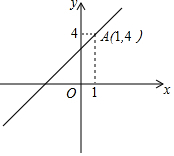 已知,一次函数y=kx+3的图象经过点A(1,4).
已知,一次函数y=kx+3的图象经过点A(1,4).
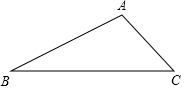 如图,在△ABC中,∠BAC是钝角,按要求画图(不写作法,保留作图痕迹,指出所求)
如图,在△ABC中,∠BAC是钝角,按要求画图(不写作法,保留作图痕迹,指出所求)