题目内容
1.下列数组不能构成直角三角形三边长的是( )| A. | 3,4,5 | B. | 5,12,13 | C. | 1,$\sqrt{2}$,$\sqrt{3}$ | D. | 2,3,4 |
分析 判断是否为直角三角形,只要验证两小边的平方和等于最长边的平方即可.
解答 解:A、32+42=52,能组成直角三角形,不符合题意;
B、52+122=132,能组成直角三角形,不符合题意;
C、12+($\sqrt{2}$)2=($\sqrt{3}$)2,能组成直角三角形,不符合题意;
D、22+32≠42,不能组成直角三角形,符合题意.
故选:D.
点评 本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.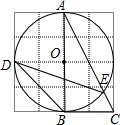 如图,边长为1的小正方形构成的网格中,半径为2的⊙O的圆心O在格点上,则∠BDE的正切值等于( )
如图,边长为1的小正方形构成的网格中,半径为2的⊙O的圆心O在格点上,则∠BDE的正切值等于( )
 如图,边长为1的小正方形构成的网格中,半径为2的⊙O的圆心O在格点上,则∠BDE的正切值等于( )
如图,边长为1的小正方形构成的网格中,半径为2的⊙O的圆心O在格点上,则∠BDE的正切值等于( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{2}$ | D. | 2 |
11.2011年成都市大约有3万名学生参加中考,为了考查他们的数学考试情况,评卷人抽取了1000名学生的数学成绩进行统计,那么下列四个判断正确的是( )
| A. | 每名学生的数学成绩是个体 | B. | 3万名学生是总体 | ||
| C. | 上述调查是普查 | D. | 1000名考生是总体的一个样本 |
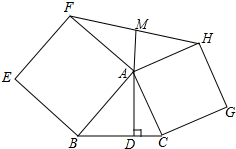 如图,分别以△ABC的边AB,AC为一边在三角形外作正方形ABEF和ACGH,M为FH上的中点,求证:MA⊥BC.
如图,分别以△ABC的边AB,AC为一边在三角形外作正方形ABEF和ACGH,M为FH上的中点,求证:MA⊥BC.